Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABC ta có
\(BC^2=\left(10a\right)^2=100a^2\)
\(AB^2+AC^2=\left(6a\right)^2+\left(8a\right)^2=100a^2\)
Từ (1) và (2) \(BC^2=AB^2+AC^2\)
Nên ΔABC vuông tại A
Xét ΔABC ta có:
\(AH\cdot BC=AB\cdot AC\)
\(\Rightarrow AH=\dfrac{AB\cdot AC}{BC}=\dfrac{8a\cdot6a}{10a}=\dfrac{48a^2}{10a}=4,8a\)
\(\Rightarrow\left|\overrightarrow{AH}\right|=AH=4,8a\)

Ta có H nằm giữa B, C nên:
\(BC=BH+CH=10+42=52\left(cm\right)\)
Xét ΔABC vuông tại A và có đường cao AH ta có:
\(AB^2=BH\cdot BC\) (cạnh góc vuông và hình chiếu)
\(\Rightarrow AB=\sqrt{BH\cdot BC}\)
\(\Rightarrow AB=\sqrt{10\cdot52}=\sqrt{520}=2\sqrt{130}\left(cm\right)\)
Mà: \(\left|\overrightarrow{AB}\right|=AB\)
\(\Rightarrow\left|\overrightarrow{AB}\right|=2\sqrt{130}\left(cm\right)\)

a: vecto AB=(-7;1)
vecto AC=(1;-3)
vecto BC=(8;-4)
b: \(AB=\sqrt{\left(-7\right)^2+1^2}=5\sqrt{2}\)
\(AC=\sqrt{1^2+\left(-3\right)^2}=\sqrt{10}\)
\(BC=\sqrt{8^2+\left(-4\right)^2}=\sqrt{80}=4\sqrt{5}\)

Dựng điểm D sao cho H là trung điểm AD.
Ta có; H là trung điểm của mỗi đường AD ; BC. Do đó, tứ giác ACDB là hình bình hành.
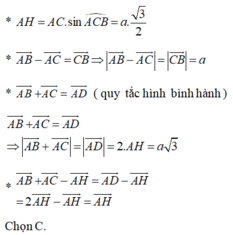

\(\widehat{HAC}=30^0\) ; \(AH=\frac{a\sqrt{3}}{2}\)
\(x=\left|\overrightarrow{AH}+\overrightarrow{AC}\right|\Rightarrow x^2=AH^2+AC^2+2\overrightarrow{AH}.\overrightarrow{AC}\)
\(\Rightarrow x^2=AH^2+AC^2+2AH.AC.cos\widehat{HAC}\)
\(\Rightarrow x^2=\left(\frac{a\sqrt{3}}{2}\right)^2+a^2+2.\frac{a\sqrt{3}}{2}.a.cos30^0\)
\(\Rightarrow x^2=\frac{13a^2}{4}x\Rightarrow x=\frac{a\sqrt{13}}{2}\)

AB^2=BH*BC
=>BH(BH+9)=20^2=400
=>BH^2+9BH-400=0
=>(BH+25)(BH-16)=0
=>BH=16cm
AH=căn BH*CH=12(cm)

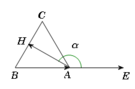
Vẽ A E → = B A → .
Vì tam giác ABC là tam giác đều nên đường cao AH đồng thời là đường phân giác.
Suy ra: B A H ^ = 1 2 B A C ^ = 30 0
Khi đó A H → , A E → = H A E ^ = α (hình vẽ)
= 180 0 − B A H ^ = 180 0 − 30 0 = 150 0 .
Chọn D.
ΔABC đều có AH là đường cao
nên \(AH=\dfrac{AB\cdot\sqrt{3}}{2}=\dfrac{2a\cdot\sqrt{3}}{2}=a\sqrt{3}\)
=>\(\left|\overrightarrow{AH}\right|=AH=a\sqrt{3}\)
Xét tam giác ABC đều có đường cao AH ta có:
\(\Rightarrow BH=HC=\dfrac{BC}{2}=\dfrac{2a}{2}=a\)
Mà: \(AH=\sqrt{AB^2-BH^2}=\sqrt{\left(2a\right)^2-a^2}\)
\(\Rightarrow AH=\sqrt{4a^2-a^2}=a\sqrt{3}\)
\(\Rightarrow\left|\overrightarrow{AH}\right|=AH=a\sqrt{3}\)