Trên mặt phẳng Oxy , cho ba điểm A(1;-4) , B(4;5) , C(0;-7) . Điểm M di chuyển trên trục Ox . Đặt Q=2|vectoMA+2vectoMB| +3|vectoMB+vectoMC| . Tìm giá trị nhỏ nhất của Q
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn A
Điểm N(x;y;0). Tìm x;y từ hệ hai phương trình NA = NB = NC.

Đáp án C
Gọi I(x;y;0) là tâm của mặt cầu (S) ⇒ A I → = x - 1 ; y - 2 ; 4 A I → = x - 1 ; y + 3 ; - 1 A I → = x - 2 ; y - 2 ; - 3
Theo bài ra, ta có
I A = I B I A = I C ⇒ x - 1 2 + y - 2 2 + 4 2 = x - 1 2 + y + 3 2 + - 1 2 x - 1 2 + y - 2 2 + 4 2 = x - 2 2 + y - 2 2 + - 3 2 ⇔ x = - 2 y = 1
Vậy I ( - 2 ; 1 ; 0 ) ⇒ A I → = ( - 3 ; - 1 ; 4 ) ⇒ l = 2 . I A = 2 16 .

Chọn C
Gọi tâm mặt cầu là: I(x;y;0).
I A = I B I A = I C ⇔ ( x - 1 ) 2 + ( y - 2 ) 2 + 4 2 = ( x - 1 ) 2 + ( y + 3 ) + 1 2 ( x - 1 ) 2 + ( y - 2 ) 2 + 4 2 = ( x - 2 ) 2 + ( y - 2 ) 2 + 3 2 ⇔ ( y - 2 ) 2 + 4 2 = ( y + 3 ) 2 + 1 2 x 2 - 2 x + 1 + 16 = x 2 - 4 x + 4 + 9 ⇔ 10 y = 10 2 x = - 4 ⇔ x = - 2 y = 1 ⇒ i = 2 R = 2 ( - 3 ) 2 + ( - 1 ) 2 + 4 2 = 2 26

ta có độ dài \(\hept{\begin{cases}AB=2\sqrt{2}\\BC=4\sqrt{2}\\CA=6\sqrt{2}\end{cases}\Rightarrow AB+BC=CA}\) vậy nên 3 diểm này thẳng hàng

AB (-1,-3)
AC (3,1)
BC (4.4)
Ta co : AB.AC= (-1).(3) + (-3).(1) = 0
suy ra : tam giac ABC vuong tai A
S= 1/2.AB.AC
Ban tu tinh do dai AB, AC nhé

E trên trục hoành nên E(x;0)
A(6;3); B(-3;6); E(x;0)
\(\overrightarrow{AB}=\left(-9;3\right);\overrightarrow{AE}=\left(x-6;-3\right)\)
Để A,B,E thẳng hàng thì \(\dfrac{x-6}{-9}=\dfrac{-3}{3}=-1\)
=>x-6=9
=>x=15
Vậy: E(15;0)
Do E thuộc trục hoành nên tọa độ có dạng \(E\left(x;0\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-9;3\right)\\\overrightarrow{AE}=\left(x-6;-3\right)\end{matrix}\right.\)
3 điểm A, B, E thẳng hàng khi:
\(\dfrac{x-6}{-9}=\dfrac{-3}{3}\Rightarrow x-6=9\)
\(\Rightarrow x=15\Rightarrow E\left(15;0\right)\)

Gọi pt đường thẳng AB có dạng y =ax + b
Tọa độ các điểm A ; B thỏa mãn pt y = ax + b nên ta có hpt :
3 = 2a + b
-3 = -a + b
.....
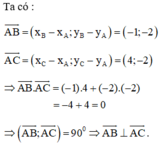
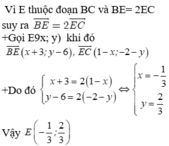
Do M thuộc Ox, gọi \(M\left(x;0\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}=\left(1-x;-4\right)\\\overrightarrow{MB}=\left(4-x;5\right)\\\overrightarrow{MC}=\left(-x;-7\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}+2\overrightarrow{MB}=\left(9-3x;6\right)\\\overrightarrow{MB}+\overrightarrow{MC}=\left(4-2x;-2\right)\end{matrix}\right.\)
\(\Rightarrow Q=2\sqrt{\left(9-3x\right)^2+5^2}+3\sqrt{\left(4-2x\right)^2+\left(-2\right)^2}\)
\(Q=2\sqrt{9\left(3-x\right)^2+25}+3\sqrt{4\left(x-2\right)^2+4}\)
\(Q=6\left(\sqrt{\left(3-x\right)^2+\dfrac{25}{9}}+\sqrt{\left(x-2\right)^2+1}\right)\)
\(Q\ge6\sqrt{\left(3-x+x-2\right)^2+\left(\dfrac{5}{3}+1\right)^2}=2\sqrt{73}\)
Vậy \(Q_{min}=2\sqrt{73}\) khi \(x=\dfrac{77}{34}\)
Sao x=77phần43 dạ thầy