Trong không gian Oxyz cho A (1;2;-1), B (3;1;-2), C (2;3;-3) và mặt phẳng (P): x-2y+2z-3=0. M (a;b;c) là điểm thuộc mặt phẳng (P) sao cho biểu thức MA²+MB²+MC² có giá trị nhỏ nhất. Xác định a+b+c. A. -3 B. -2 C. 2 D. 3...
Đọc tiếp
Trong không gian Oxyz cho A (1;2;-1), B (3;1;-2), C (2;3;-3) và mặt phẳng (P): x-2y+2z-3=0. M (a;b;c) là điểm thuộc mặt phẳng (P) sao cho biểu thức MA²+MB²+MC² có giá trị nhỏ nhất. Xác định a+b+c.
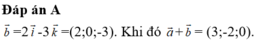
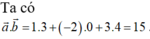
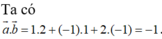
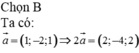
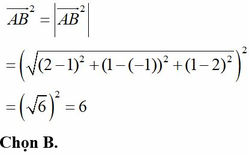
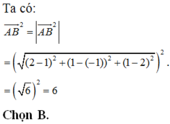
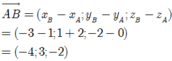
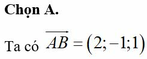
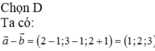
Chọn D
Gọi G (2;2;-2) là trọng tâm tam giác ABC, khi đó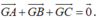
Ta có:
đạt giá trị nhỏ nhất khi M là hình chiếu vuông góc của G trên mặt phẳng (P). Khi đó tọa độ của M (a;b;c) và vecto
cùng phương với vecto pháp tuyến n (1;-2;2) thỏa mãn hệ 
Vậy a+b+c=3.