Ta có : \(\sqrt{25}=5;-\sqrt{25}=-5;\sqrt{\left(-5\right)^2}=\sqrt{25}=5\)
Theo mẫu trên, hãy tính :
a) \(\sqrt{36}\)
b) \(-\sqrt{16}\)
c) \(\sqrt{\dfrac{9}{25}}\)
d) \(\sqrt{3^2}\)
e) \(\sqrt{\left(-3\right)^2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LM
3 tháng 9 2016
a) \(\sqrt{36}=6\)
b)\(-\sqrt{16}=-4\)
c)\(\sqrt{\frac{9}{25}}=\frac{3}{5}\)
d)\(\sqrt{3^2}=\sqrt{9}=3\)
e)\(\sqrt{\left(-3\right)^2}=\sqrt{9}=3\)
B
2
AQ
3 tháng 12 2023
Bạn đang tìm kiếm số tự nhiên n để biểu thức: sqrt(5 + sqrt(25 - n)) + sqrt(5 - sqrt(25 - n)) có giá trị nguyên. Để giải quyết vấn đề này, chúng ta sẽ sử dụng một số tính chất của các số nguyên và căn bậc hai.
Đầu tiên, ta nhận thấy rằng nếu biểu thức trên có giá trị nguyên, thì cả hai căn bậc hai phải là số nguyên. Điều này có nghĩa là 5 + sqrt(25 - n) và 5 - sqrt(25 - n) đều phải là bình phương của một số nguyên. Ta có thể viết lại hai biểu thức này như sau:
5 + sqrt(25 - n) = a^2 5 - sqrt(25 - n) = b^2
Trong đó a và b là các số nguyên. Từ đó, ta có:
a^2 + b^2 = 10 a^2 - b^2 = sqrt(25 - n)
Ta có thể giải hệ phương trình này để tìm a, b, và n. Đầu tiên, ta có:
(a^2 + b^2) + (a^2 - b^2) = 2a^2 = 10 + sqrt(25 - n)
Từ đó, ta suy ra:
a^2 = 5 + (1/2)sqrt(25 - n)
Tương tự, ta có:
b^2 = 5 - (1/2)sqrt(25 - n)
Do a và b là các số nguyên, ta có thể suy ra rằng sqrt(25 - n) phải là một số chẵn. Từ đó, ta có:
25 - n = 4k^2
Với k là một số nguyên. Từ đó, ta suy ra:
n = 25 - 4k^2
Vậy để biểu thức sqrt(5 + sqrt(25 - n)) + sqrt(5 - sqrt(25 - n)) có giá trị nguyên, thì n phải là một số tự nhiên sao cho sqrt(25 - n) là một số chẵn. Các giá trị của n thỏa mãn điều kiện này là n = 3 và n = 7 1.
Vì vậy, để biểu thức sqrt(5 + sqrt(25 - n)) + sqrt(5 - sqrt(25 - n)) có giá trị nguyên, thì n phải là một trong hai số tự nhiên 3 hoặc 7.
AQ
3 tháng 12 2023
Bạn đang tìm kiếm số tự nhiên n để biểu thức: sqrt(5 + sqrt(25 - n)) + sqrt(5 - sqrt(25 - n)) có giá trị nguyên. Để giải quyết vấn đề này, chúng ta sẽ sử dụng một số tính chất của các số nguyên và căn bậc hai.
Đầu tiên, ta nhận thấy rằng nếu biểu thức trên có giá trị nguyên, thì cả hai căn bậc hai phải là số nguyên. Điều này có nghĩa là 5 + sqrt(25 - n) và 5 - sqrt(25 - n) đều phải là bình phương của một số nguyên. Ta có thể viết lại hai biểu thức này như sau:
5 + sqrt(25 - n) = a^2 5 - sqrt(25 - n) = b^2
Trong đó a và b là các số nguyên. Từ đó, ta có:
a^2 + b^2 = 10 a^2 - b^2 = sqrt(25 - n)
Ta có thể giải hệ phương trình này để tìm a, b, và n. Đầu tiên, ta có:
(a^2 + b^2) + (a^2 - b^2) = 2a^2 = 10 + sqrt(25 - n)
Từ đó, ta suy ra:
a^2 = 5 + (1/2)sqrt(25 - n)
Tương tự, ta có:
b^2 = 5 - (1/2)sqrt(25 - n)
Do a và b là các số nguyên, ta có thể suy ra rằng sqrt(25 - n) phải là một số chẵn. Từ đó, ta có:
25 - n = 4k^2
Với k là một số nguyên. Từ đó, ta suy ra:
n = 25 - 4k^2
Vậy để biểu thức sqrt(5 + sqrt(25 - n)) + sqrt(5 - sqrt(25 - n)) có giá trị nguyên, thì n phải là một số tự nhiên sao cho sqrt(25 - n) là một số chẵn. Các giá trị của n thỏa mãn điều kiện này là n = 3 và n = 7 1.
Vì vậy, để biểu thức sqrt(5 + sqrt(25 - n)) + sqrt(5 - sqrt(25 - n)) có giá trị nguyên, thì n phải là một trong hai số tự nhiên 3 hoặc 7.
5 tháng 10 2023
`#3107.101107`
a)
`2/5 \sqrt{25} - 1/2 \sqrt{4}`
`= 2/5 * \sqrt{5^2} - 1/2 * \sqrt{2^2}`
`= 2/5*5 - 1/2*2`
`= 2 - 1`
`= 1`
b)
`0,5*\sqrt{0,09} + 5*\sqrt{0,81}`
`= 0,5*\sqrt{(0,3)^2} + 5*\sqrt{(0,9)^2}`
`= 0,5*0,3 + 5*0,9`
`= 0,15 + 4,5`
`= 4,65`
c)
`2/5\sqrt{25/36} - 5/2\sqrt{4/25}`
`= 2/5*\sqrt{(5^2)/(6^2)} - 5/2*\sqrt{(2^2)/(5^2)}`
`= 2/5*5/6 - 5/2*2/5`
`= 1/3 - 1`
`= -2/3`
d)
`-2 \sqrt{(-36)/(-16)} + 5 \sqrt{(-81)/(-25)}`
`= -2*\sqrt{36/16} + 5*\sqrt{81/25}`
`= -2*\sqrt{(6^2)/(4^2)} + 5*\sqrt{(9^2)/(5^2)}`
`= -2*6/4 + 5*9/5`
`= -3 + 9`
`= 6`
7L
4
PT
1
PT
1
a)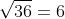
;
b)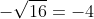
;
c)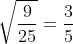
;
d)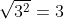
;
e)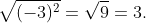
a) \(\sqrt{36}=6\)
b) \(-\sqrt{16}=-4\)
c) \(\sqrt{\dfrac{9}{25}}=\dfrac{\sqrt{9}}{\sqrt{25}}=\dfrac{3}{5}\)
d) \(\sqrt{3^2}=3\)
e) \(\sqrt{\left(-3\right)^2}=\sqrt{9}=3\)