Cho x>0; y>0 và x^2+y^2 <=x+y. Giá trị lớn nhất của biểu thức A=x+3y là..........
ai lam dum' cho 3 tick cho ng' som nhat
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt 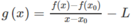
Suy ra g(x) xác định trên
(
a
;
b
)
\
x
0
và 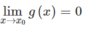
Mặt khác, f ( x ) = f ( x 0 ) + L ( x − x 0 ) + ( x − x 0 ) g ( x ) nên
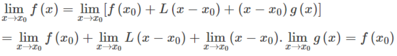
Vậy hàm số y = f(x) liên tục tại

Đáp án A
Phương pháp:
Dựa vào khái niệm cực trị và các kiến thức liên quan.
Cách giải:
(1) chỉ là điều kiện cần mà không là điều kiện đủ.
VD hàm số y = x3 có y' = 3x2 = 0 ⇔ x = 0. Tuy nhiên x = 0 không là điểm cực trị của hàm số.
(2) sai, khi f''(x0) = 0, ta không có kết luận về điểm x0 có là cực trị của hàm số hay không.
(3) hiển nhiên sai.
Vậy (1), (2), (3): sai; (4): đúng

Dễ thấy: \(x_0;y_0\ne 0\)
*)Xét \(x_0;y_0>0\) xài BĐT AM-GM
\(x^3+y^3+1\ge3\sqrt[3]{x^3y^3}=3xy\)
Xảy ra khi \(x=y=1\)
Khi đó \(\left(1+x_0\right)\left(1+\dfrac{1}{y_0}\right)\left(1+\dfrac{x_0}{y_0}\right)=8\)
*)Xét \(x_0;y_0<0\)\(\Rightarrow3xy>0;x^3+y^3+1\le0\) (loại)

- Định nghĩa:
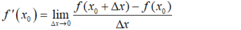
- Cho h = Δx, khi Δx → 0 thì h → 0 nên ta có:
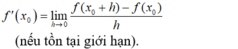
Chọn C

Ta có
x − y = 5 3 x + 2 y = 18 ⇔ x = y + 5 3. y + 5 + 2 y = 18 ⇔ x = y + 5 3 y + 15 + 2 y = 18 ⇔ x = y + 5 5 y = 3
⇔ y = 3 5 x = 5 + 3 5 ⇔ x = 28 5 y = 3 5
Vậy hệ phương trình có nghiệm duy nhất x ; y = 28 5 ; 3 5 ⇒ x . y = 84 25
Đáp án: B