Cho hai vật m 1 = 16 k g ; m 2 = 4 k g .Đặt tại hai điểm AB cách nhau 20 cm, xác định vị trí đặt m 3 = 4 k g ở đâu để lực hấp dẫn giữa chúng cân bằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Các số có căn bậc hai:
a = 0 c = 1 d = 16 + 9
e = 32 + 42 h = (2-11)2 i = (-5)2
l = √16 m = 34 n = 52 - 32
Căn bậc hai không âm của các số đó là:
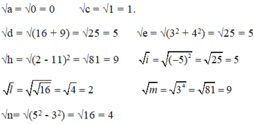

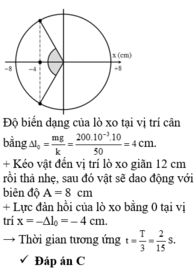
Đáp án C.
– Để vật m không rời khỏi đĩa M thì áp lực của m lên đĩa phải lớn hơn hoặc bằng lực quán tính cực đại tác dụng lên m:
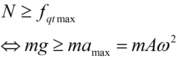

![]()

m1=400g=0,4kg
m2=300g=0,3kg
\(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\)
hai vật chuyển động vuông gốc nên
\(p=\sqrt{p_1^2+p_2^2}=\sqrt{\left(m_1.v\right)^2+\left(m_2.v\right)^2}\)=5kg.m/s

m=200g=0,2kg
l0=16cm=0,16m
\(F_{đh}\) đóng vai trò Fht
đề lò xo giản 0,04m
\(F_{ht}=F_{đh}\Leftrightarrow m.\omega^2.R=k.\Delta l\)
R bằng chiều dài l0 của lò xo
\(\Rightarrow\omega=\sqrt{\dfrac{k.\Delta l}{R.m}}\)=\(5\sqrt{5}\) (rad/s)

Gọi khối tâm của 2 vật là O.
Ta chia lò xo thành 2 đoạn $l_1, l_2$
Ta có:$\dfrac{l_1}{l_2} = \dfrac{m_2}{m_1} = \dfrac{5}{3}$
Khi đó ta sẽ chia lò xo cũ thành 2 lò xo mới: $m_1$ dao động với lò xo $l_1$
Có $\dfrac{k_1}{k} = \dfrac{8}{5}$ suy ra chu kì của vật 1 là $T_1 = 2\pi \sqrt{\dfrac{m_1}{k_1}}$.
Sau đó làm tương tự với lò xo 2 và vật $m_2$

Chọn mốc thế năng tại vị trí lò xo cân bằng
Cơ năng vị trí ban đầu:
\(W=\frac{1}{2}kx^2=\frac{1}{2}.200.0,3^2=9\left(J\right)\)
Cơ năng của vật sau khi bị nén:
\(W'=\frac{1}{2}kx'^2=100x'^2\)
Do có ma sát nên biến thiên cơ năng bằng công của lực ma sát:
\(-F_{ms}.\left(x+x'\right)=W'-W\)
\(\Leftrightarrow-0,2.10\left(0,3+\left|x'\right|\right)=100x'^2-9\)
\(\Leftrightarrow-0,6-2\left|x'\right|=100x'^2-9\)
\(\Leftrightarrow\left[{}\begin{matrix}x'=0,28\\x'=-0,3\left(l\right)\end{matrix}\right.\)
Cơ năng sau khi giãn:
\(W''=\frac{1}{2}.200.x''^2\)
\(\Rightarrow100x''^2-100x'^2=0,2.10.\left(x'+\left|x''\right|\right)\)
\(\Leftrightarrow100x''^2-100.0,28^2=0,2.10.\left(0,28+\left|x''\right|\right)\)
\(\Leftrightarrow100x''^2-2\left|x''\right|-8,4=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x''=0,3\\x''=-0,28\left(l\right)\end{matrix}\right.\) \(\Rightarrow x''=0,3\left(m\right)\)
b/ Vận tốc lớn nhất<=> Động năng lớn nhất<=> Vị trí ko có thế năng => Vị trí cân bằng
\(\frac{1}{2}mv^2-\frac{1}{2}kx''^2=-2.x''\)
\(\Leftrightarrow\frac{1}{2}v^2-\frac{1}{2}.200.0,3^2=-2.0,3\Leftrightarrow v=\frac{2\sqrt{105}}{5}\left(m/s\right)\)

2. Vật sáng AB đặt trên trục chính và vuông góc với trục chính thấu kính hội tụ cho ảnh ảo cao gấp 2 lần AB và cách thấu kính 16 cm. Tìm tiêu cự thấu kính
+ Ảnh ảo cao gấp 3 lần vật => \(\frac{h}{h'}=\frac{1}{2}=\frac{d}{d'}\rightarrow d'=2d\)
+ Do ảnh là ảnh ảo, sử dụng công thức thấu kính:
\(\frac{1}{f}=\frac{1}{d}-\frac{1}{d'}\)
→\(f=\frac{d'.d}{d'-d}=\frac{2d.d}{2d-d}=\frac{2}{1}d=\frac{2}{1}.16=32cm\)
Hình tự vẽ

Theo điều kiện cân bằng F 13 → + F 23 → = 0 ⇒ F 13 → ↑ ↓ F 23 → F 13 = F 23
Vậy m3 phải đặt trong khoảng hai vật và đặt trên đường thẳng nối hai vật
Gọi x là khoảng cách từ vật m 1 đến m 3 thì khoảng cách từ m 2 đến m 3 là 0,2 – x
F 13 = F 23 ⇒ G m 1 m 3 x 2 = G m 2 m 3 ( 0 , 2 − x ) 2 ⇒ m 1 x 2 = m 2 ( 0 , 2 − x ) 2
⇒ 16 x 2 = 4 ( 0 , 2 − x ) 2 ⇒ 4 ( 0 , 2 − x ) 2 = x 2 ⇒ 2 ( 0 , 2 − x ) = x 2 ( 0 , 2 − x ) = − x
⇒ x = 0 , 4 3 m = 40 3 c m < 20 ( T / M ) x = 0 , 4 m = 40 c m > 20 ( L )