Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo bài ra ta có:
W=Wđ+Wt =1/2.m.v2 +1/2.k.x2= 5.1/2.k.x2
Khi wt =4wđ thì cơ năng ở đó là:
w=wđ+wt = 5/4.wt = 5/4.1/2.kx'2
Theo định luật bảo toàn cơ năng cho hai vị trí ta có:
5/4.1/2.kx'^2 = 5.1/2.k.x^2 -> x' = ...

ΔL=L-L0=25-21=4cm=0.04m
tìm P=Fk=m.g=0,2.10=2
đồng thời Fk=Fđh=2N
ta có Fđh=k.ΔL
2 =k.0.04
=>k=50
b/ta có ΔL=27-21=6cm=0.06m
Fdh=k.ΔL=50.0.06=3N
=>P=Fdh=3N
=>3=10.m
m=0.3 Kg
vậy khối lượng vật treo thêm = 0.3-.02=0.1 KG

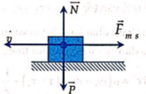
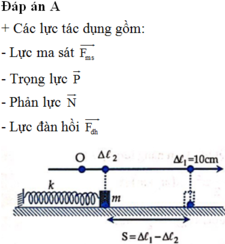
+ Khi tính công ta chú ý rằng không tính công của lực đàn hồi. Do vậy ta có:
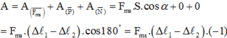
Do vật chịu tác dụng thêm lực ma sát cơ năng của vật sẽ biến đổi. Công của các lực cản bằng độ biến thiên cơ năng của vật:
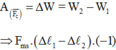
![]()
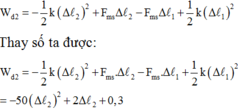
Để vận tốc lớn nhất tức là vế phải là tam thức bậc 2 lớn nhất khi đó ta được:
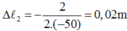

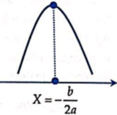

Đáp án B
+ Do bỏ qua ma sát nên cơ năng của con lắc lò xo bảo toàn.
+ Khi vmax = 100cm/s thì động năng lớn nhất thế năng bằng O. '
+ Theo bảo toàn cơ năng ta có:
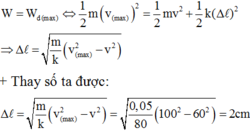

Đáp án D
Ta giải nhanh khi đã nắm được công thức:
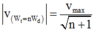
Ở bài toán này: Động năng bằng 1/3 lần thế năng
<=> thế năng bằng 3 lần động năng
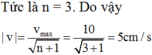

Áp dụng định luật hai Newton lên vật m1
\(\overrightarrow{F_1}+\overrightarrow{N_1}+\overrightarrow{P_1}=m_1\overrightarrow{a_1}\)
\(\Rightarrow F_1=m_1a_1\)
Áp dụng định luật hai Newton lên vật m2
\(\overrightarrow{F_2}+\overrightarrow{N_2}+\overrightarrow{P_2}=m_2\overrightarrow{a_2}\)
\(\Rightarrow F_2=m_2a_2\)
Lại có: \(F_1=F_2\Rightarrow m_1a_1=m_2a_2\)
Mà \(a=\dfrac{2s}{t^2}\)
\(\Rightarrow m_1s_1=m_2s_2\)
\(\Leftrightarrow m_1=3m_2\) (1)
Có: \(m_1+m_2=3\) (2)
Từ (1) và (2) giải hệ phương trình ta được: \(\left\{{}\begin{matrix}m_1=3\left(kg\right)\\m_2=1\left(kg\right)\end{matrix}\right.\)

Độ dãn tối đa \(\Delta l_o=\frac{mg}{k}\)
Vận tốc lớn nhất \(v_{max}=\omega A=\sqrt{\frac{k}{m}}\frac{mg}{k}=g\sqrt{\frac{m}{k}}\)
 10
10
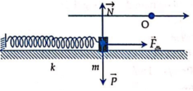
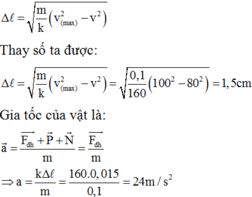
Chọn mốc thế năng tại vị trí lò xo cân bằng
Cơ năng vị trí ban đầu:
\(W=\frac{1}{2}kx^2=\frac{1}{2}.200.0,3^2=9\left(J\right)\)
Cơ năng của vật sau khi bị nén:
\(W'=\frac{1}{2}kx'^2=100x'^2\)
Do có ma sát nên biến thiên cơ năng bằng công của lực ma sát:
\(-F_{ms}.\left(x+x'\right)=W'-W\)
\(\Leftrightarrow-0,2.10\left(0,3+\left|x'\right|\right)=100x'^2-9\)
\(\Leftrightarrow-0,6-2\left|x'\right|=100x'^2-9\)
\(\Leftrightarrow\left[{}\begin{matrix}x'=0,28\\x'=-0,3\left(l\right)\end{matrix}\right.\)
Cơ năng sau khi giãn:
\(W''=\frac{1}{2}.200.x''^2\)
\(\Rightarrow100x''^2-100x'^2=0,2.10.\left(x'+\left|x''\right|\right)\)
\(\Leftrightarrow100x''^2-100.0,28^2=0,2.10.\left(0,28+\left|x''\right|\right)\)
\(\Leftrightarrow100x''^2-2\left|x''\right|-8,4=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x''=0,3\\x''=-0,28\left(l\right)\end{matrix}\right.\) \(\Rightarrow x''=0,3\left(m\right)\)
b/ Vận tốc lớn nhất<=> Động năng lớn nhất<=> Vị trí ko có thế năng => Vị trí cân bằng
\(\frac{1}{2}mv^2-\frac{1}{2}kx''^2=-2.x''\)
\(\Leftrightarrow\frac{1}{2}v^2-\frac{1}{2}.200.0,3^2=-2.0,3\Leftrightarrow v=\frac{2\sqrt{105}}{5}\left(m/s\right)\)