Cho tứ giác ABCD có AB=BC=CD; góc AOD =a(O là giao điểm của hai đường chéo). Các tia phân giác của góc A và D cắt nhau tại I. Tính góc AID theo a.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 11 2022
1/nối AC
Do AB//CD=>BAC=ACD(so le trong)
Do AD//BC=>ACB=DAC(so le trong)
Xét ∆ABC và ∆ACD
ACB=DAC(chứng minh trên)
BAC=DAC(chứng minh trên)
AC chung
Vậy ∆ABC=∆CDA(g.c.g)=>AB=DC(cặp cạnh tương ứng)
AD=BC(cặp cạnh tương ứng)
25 tháng 7 2017
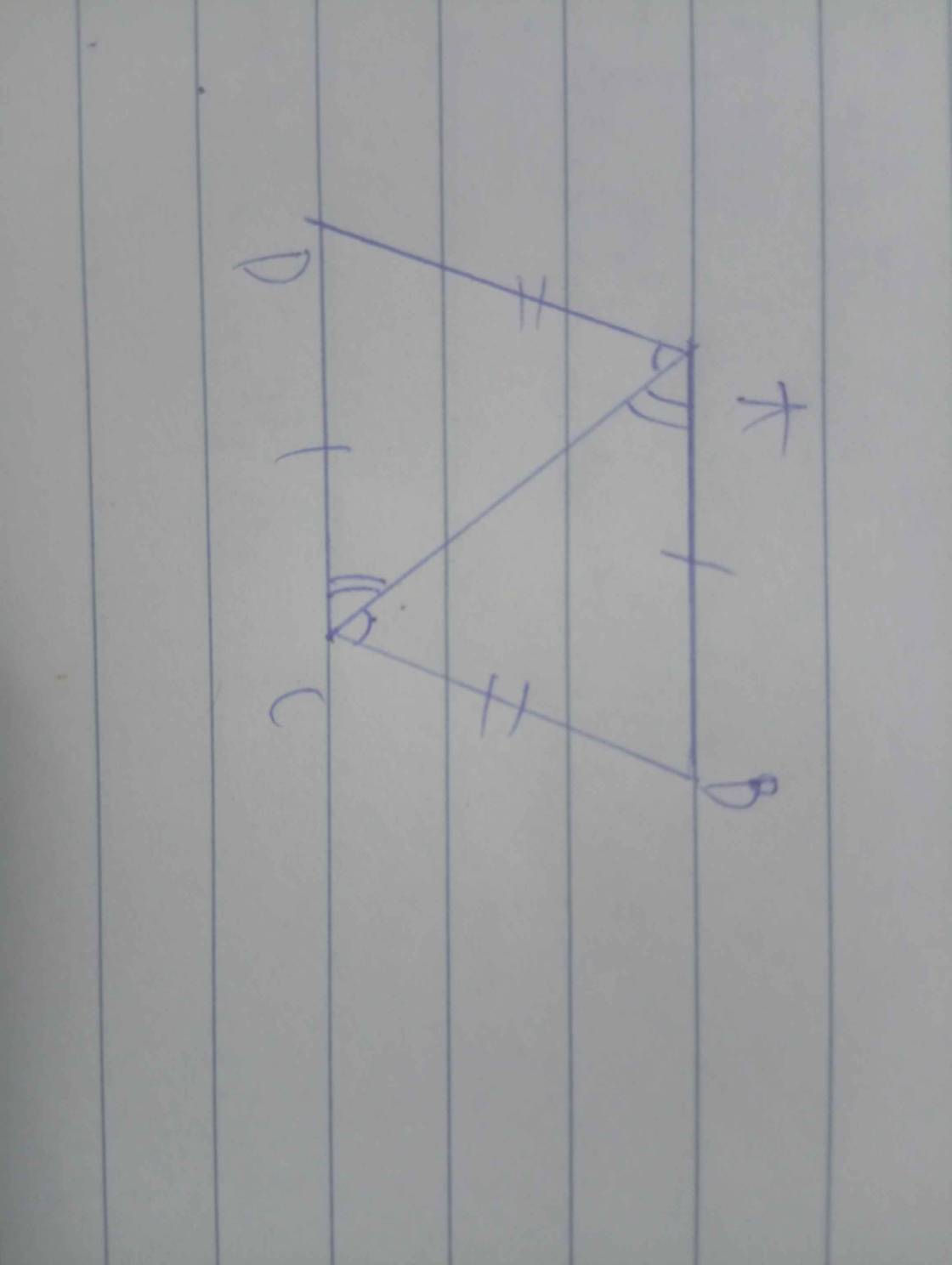
AB = 5cm
=> BC = 12 - 5 = 7cm
=> CD = 12 - 7 = 5cm
=> AD = 12 - 5 = 7cm
Vì AB = CD, BC = AD, mà AB đối CD, BC đối AD
=> Tứ giác ABCD là hbh
10 tháng 7 2021
Bạn xem hình vẽ ở đây nhé: https://i.imgur.com/sh8KysD.png
Gọi CD giao AB tại O, Đặt OD=a, OA=b.
Xét tam giác OAD vuông tại O ta có
a^2 + b^2 =25
Xét tam giác OBC vuông tại O ta có
(a+8^2 )+ (b+2^2=13^2
Từ đó tính được a=84/17 hoặc a=4. Loại a=84/17vì với a=84/17 thì b<0
Với a=4 suy ra b=3. Khi đó SABCD=SOBC-SOAD=24
AT
10 tháng 7 2021
Bạn xem hình vẽ ở đây nhé: https://i.imgur.com/sh8KysD.png
Gọi CD giao AB tại O, Đặt OD=a, OA=b.
Xét tam giác OAD vuông tại O ta có \(a^2+b^2=25\)
Xét tam giác OBC vuông tại O ta có \(\left(a+8\right)^2+\left(b+2\right)^2=13^2\)
Từ đó tính được a \(=\frac{87}{17}\)hoặc a = 4. Loại a = \(\frac{87}{17}\)vì với a = \(\frac{87}{17}\) thì \(b< 0\)
Với a = 4 suy ra b = 3. Khi đó \(^SABCD=^SOBC-^SOAD=24\)
PG
2
9 tháng 12 2021
Xét tứ giác ABCD có
AB//CD
AD//BC
DO đó: ABCD là hình bình hành
Suy ra: AB=CD; AD=BC
YN
0
và 
. 
và 
.
BD
3
7 tháng 9 2017
Chứng minh rằng AK=KC,BI=ID
vì FE là đường trung bình hình thang nên FE//AB//CD
E, F là trung điểm của AD và BC nên AK=KC
BI=ID
( trong tam giác đường thẳng qua trung điểm của 1 cạnh, // với cạnh thứ 2 thì qua trung điểm cạnh thứ 3)
7 tháng 9 2017
Xét t/g ABC và t/g CDA có :
AC cạnh chung
AB = CD ( gt )
\(\widehat{A1}=\widehat{C1}\)( slt , AB // CD )
\(\Rightarrow\)t/g ABC = t/g CDA ( c-g-c )
\(\Rightarrow\)BC = AD
\(\widehat{A2}=\widehat{C2}\) và 2 góc này ở vị trí slt
\(\Rightarrow\)BC // AD
3 tháng 4 2023
AB=BM
nên \(S_{QAB}=S_{QBM}\)
DA=AQ
=>\(S_{BDA}=S_{BAQ}\)
=>\(S_{QAM}=2\cdot S_{ABD}\)
Tương tự, ta được: \(S_{MBN}=2\cdot S_{ABC};S_{NCP}=2\cdot S_{BCD};S_{PDQ}=2\cdot S_{ADC}\)
=>\(S_{MNPQ}=5\cdot S_{ABCD}=300\left(cm^2\right)\)
22 tháng 2 2022
1: Ta có:ABCD là hình chữ nhật
nên AB=CD;AD=BC
2: Xét tứ giác ABCD có
AB=CD
AD=BC
Do đó: ABCD là hình bình hành
Xét ΔADE và ΔCBF có
\(\widehat{D}=\widehat{B}\)
AD=CB
\(\widehat{DAE}=\widehat{BCF}\)
Do đó: ΔADE=ΔCBF
Suy ra: \(\widehat{AED}=\widehat{CFB}\)
=>\(\widehat{AEC}=\widehat{CFA}\)
Xét tứ giác AECF có
\(\widehat{AEC}=\widehat{CFA}\)
\(\widehat{FAE}=\widehat{FCE}\)
Do đó: AECF là hình bình hành
Suy ra: AE//CF