Câu 1 : Trong mặt phẳng tọa độ Oxy ; cho (E) : x^2/a^2 + y^2/b^2 = 1 ( a > b > 0 ) . Một góc vuông uOv ( vuông tại O ) , cắt (E) tại M ; N . CMR : 1/OM^2 + 1/ON^2 ko đổi . Từ đó suy ra MN luôn tiếp xúc với 1 đường tròn cố định
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(1); vecto u=2*vecto a-vecto b
=>\(\left\{{}\begin{matrix}x=2\cdot1-0=2\\y=2\cdot\left(-4\right)-2=-10\end{matrix}\right.\)
(2): vecto u=-2*vecto a+vecto b
=>\(\left\{{}\begin{matrix}x=-2\cdot\left(-7\right)+4=18\\y=-2\cdot3+1=-5\end{matrix}\right.\)
(3): vecto a=2*vecto u-5*vecto v
\(\Leftrightarrow\left\{{}\begin{matrix}a=2\cdot\left(-5\right)-5\cdot0=-10\\b=2\cdot4-5\cdot\left(-3\right)=15+8=23\end{matrix}\right.\)
(4): vecto OM=(x;y)
2 vecto OA-5 vecto OB=(-18;37)
=>x=-18; y=37
=>x+y=19

1, Gọi tọa độ điểm D(x;y)
Ta có:\(\overrightarrow{AB}\left(8;1\right)\)
\(\overrightarrow{DC}\left(1-x;5-y\right)\)
Tứ giác ABCD là hình bình hành khi
\(\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Leftrightarrow1-x=8;5-y=1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-7\\y=4\end{matrix}\right.\)
Vậy tọa độ điểm D(-7;4)

\(\overrightarrow{AB}=\left(x_B-x_A;y_B-y_A\right)=\left(3;-9\right)\)

a: 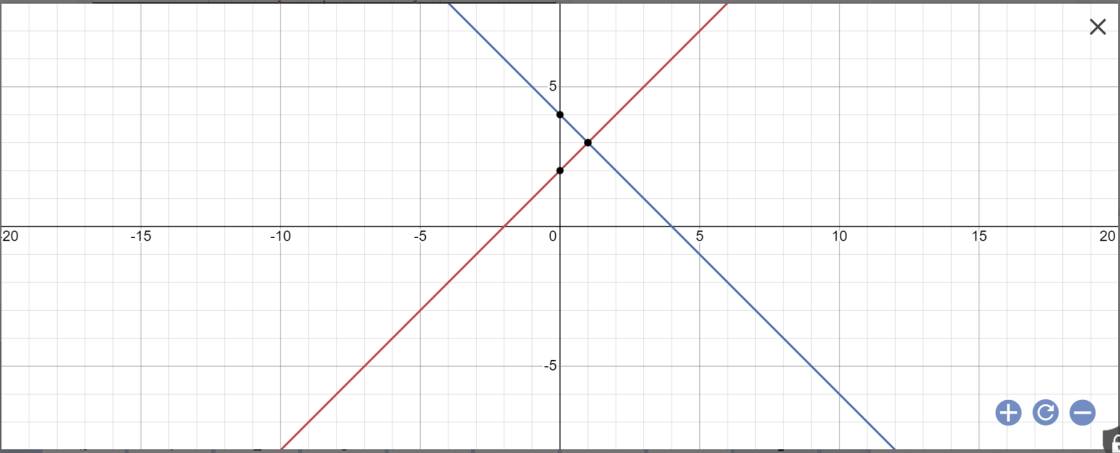
b: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}x+2=-x+4\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=2\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1+2=3\end{matrix}\right.\)
Thay x=1 và y=3 vào (d3), ta được:
\(1\cdot m+m=3\)
=>2m=3
=>\(m=\dfrac{3}{2}\)

Có vô số điểm N để A,B,N thẳng hàng, cho nên để tìm ra 1 điểm N cụ thể thì cần thêm điều kiện nữa (ví dụ N thuộc Ox, Oy hoặc đường thẳng nào đó)
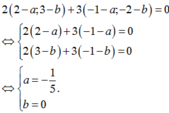
Vì \(Ou\perp Ov\) nên giả sử PTĐT Ou và Ov lần lượt là : \(y=kx;y=-\dfrac{1}{k}x\) ( \(k\ne0\) )
Giả sử \(Ou;Ov\cap\left(E\right)\) lần lượt tại M ; N
Xét PTHĐGĐ của Ou và \(\left(E\right)\) là no của pt : \(\dfrac{x^2}{a^2}+\dfrac{k^2x^2}{b^2}=1\)
\(\Leftrightarrow\dfrac{x^2\left(b^2+k^2a^2\right)}{a^2b^2}=1\) \(\Leftrightarrow x_M^2=\dfrac{a^2b^2}{b^2+k^2a^2}\)
Thấy : \(OM^2=x_M^2+y_M^2=x_M^2\left(1+k^2\right)=\dfrac{a^2b^2}{b^2+k^2a^2}\left(k^2+1\right)\)
Suy ra : \(\dfrac{1}{OM^2}=\dfrac{b^2+k^2a^2}{a^2b^2\left(k^2+1\right)}\)
Tương tự , ta có : \(\dfrac{1}{ON^2}=\dfrac{b^2+\dfrac{1}{k^2}a^2}{a^2b^2\left(\dfrac{1}{k^2}+1\right)}=\dfrac{b^2k^2+a^2}{a^2b^2\left(1+k^2\right)}\)
Suy ra : \(\dfrac{1}{OM^2}+\dfrac{1}{ON^2}=\dfrac{\left(a^2+b^2\right)\left(k^2+1\right)}{a^2b^2\left(k^2+1\right)}=\dfrac{a^2+b^2}{a^2b^2}\) ko đổi do a ; b ko đổi
Gọi H là h/c của O lên MN ; ta có : \(\dfrac{1}{OH^2}=\dfrac{1}{OM^2}+\dfrac{1}{ON^2}=\dfrac{a^2+b^2}{a^2b^2}\)
\(\Rightarrow OH^2=\dfrac{a^2b^2}{a^2+b^2}\Rightarrow OH=\dfrac{ab}{\sqrt{a^2+b^2}}\) ko đổi ( a > b > 0 )
Vì OH \(\perp\) MN nên MN luôn tiếp xúc với \(\left(O;\dfrac{ab}{\sqrt{a^2+b^2}}\right)\) cố định ( đpcm )