so sánh a = 108+2\108-1 ; b = 108\108-3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
0H
1
17 tháng 10 2021
\(B=10^{32}-1=\left(10-1\right)\left(10+1\right)\left(10^2+1\right)\left(10^4+1\right)\left(10^8+1\right)\left(10^{16}+1\right)\left(10^{32}+1\right)>\left(10+1\right)\left(10^2+1\right)\left(10^4+1\right)\left(10^8+1\right)\left(10^{16}+1\right)\left(10^{32}+1\right)=A\)Vậy B>A
2 tháng 2 2023
Ta có:
A = \(\dfrac{10^7+5}{10^7-8}=\dfrac{10^7-8+13}{10^7-8}=1+\dfrac{13}{10^7-8}\)
\(B=\dfrac{10^8+6}{10^8-7}=\dfrac{10^8-7+13}{10^8-7}=1+\dfrac{13}{10^8-7}\)
Mà \(10^8-7>10^7-8\)
=> \(1+\dfrac{13}{10^7-8}>1+\dfrac{13}{10^8-7}\)
=> A < B
Vậy A < B
2 tháng 2 2023
Xin lỗi mình kết luận sai vì nhìn nhầm. Đáp án đúng là A > B và cả quá trình trên vẫn đúng nha.
28 tháng 4 2018
Bài tích có chữ số tận cùng là 1
A= (108+2)(108-2)=108*108 +2*108-2*108-4=B-4 => A<B
QN
1
E
0
SY
3
WC
23 tháng 6 2016
107+5/107-8 -1=13/107-8
108+6/108-7 -1=13/108-7
Ta thấy 13/107-8>13/108-7=> 107+5/107-8>108+6/108-7
ND
2
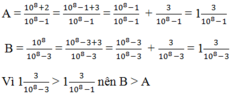
Áp dụng a/b > 1 => a/b > a+m/b+m (a,b,m thuộc N*)
Ta có:
\(b=\frac{10^8}{10^8-3}>\frac{10^8+2}{10^9-3+2}\)
\(b>\frac{10^8+2}{10^9-1}=a\)
=> b > a
so sánh a = 108+2\108-1 ; b = 108\108-3
BL:
Áp dụng a/b > 1 => a/b > a+m/b+m (a,b,m thuộc N*)
Ta có:
b=108/108−3 >108+2/109−3+2
b>108+2/109−1 =a
=> b > a