Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh A; S A ⊥ A B C và S A = a 3 . Tính góc giữa đường thẳng SB với mặt phẳng (ABC)
A. 75 °
B. 60 °
C. 45 °
D. 30 °
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 9 2018
Đáp án A
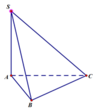
Do tam giác ABC đều cạnh a nên có S ∆ A B C = a 2 3 4
⇒ V = 1 3 S A . S ∆ A B C = 1 3 . a 6 . a 2 3 4 = a 2 2 4
CM
26 tháng 6 2019
Chọn C.
Diện tích ∆ ABC là S A B C = a 2 3 4
SA ⊥ (ABC) nên SA là chiều cao của hình chóp và SA= a 3
Thể tích khối chóp là
V = 1 3 S A B C . S A = 1 3 . a 2 3 4 . a 3 = a 3 4
CM
21 tháng 6 2019
Đáp án C
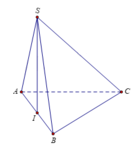
Gọi I là trung điểm của A B ⇒ S I ⊥ A B C
Ta có S I = a 2 − a 2 2 = a 3 2 ; S A B C = 1 2 a 2 sin 60 ° = a 2 3 4
Thể tích của khối chóp S . A B C là:
V = 1 3 S I . S A B C = 1 3 . a 3 2 . a 2 3 4 = a 3 8
CM
5 tháng 8 2019
Đáp án B
Ta có: O là giao điểm của trục đường tròn ngoại tiếp tam giác ABC và SAB.
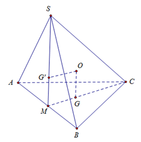
Ta có: O G = 1 3 S M = 3 6 ; M G = C M 3 = 3 6
R = S O = M G 2 + S G 2 = 3 6 + 1 3 = 15 6
Cách 2: Áp dụng CT giải nhanh trong trường hợp S A B ⊥ A B C ta có:
R 2 = R 2 A B C + R 2 S A B − A B 2 4 = 1 2 3 + 1 2 3 − 1 4 = 2 3 − 1 4 = 5 12 ⇒ R = 15 6 .
Vậy V = 4 3 π R 3 = 5 15 π 54 .
Đáp án B