Câu 4: Cho góc nhọn xOy. Lấy M là một điểm nằm trên tia phân giác Ot của góc xOy. Kẻ MQ \(\perp\)Ox ( Q \(\in\)Ox ) ; MH \(\perp\)Oy ( H \(\in\)Oy )
a) CM: MQ = MH
b) Nối QH cắt Ot ở G. CM : GQ = GH
c) CM: QH \(\perp\)OM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 12 2016
Kí hiệu tam giác là t/g
a) Xét t/g QOM vuông tại Q và t/g HOM vuông tại H có:
OM là cạnh chung
QOM = HOM ( vì OM là p/g của HOQ)
Do đó, t/g QOM = t/g HOM ( cạnh huyền và góc nhọn kề)
=> MQ = MH (2 cạnh tương ứng) (đpcm)
b) t/g QOM = t/g HOM (câu a)
=> QMO = HMO (2 góc tương ứng)
Xét t/g QMG và t/g HMG có:
MG là cạnh chung
QMG = HMG (cmt)
MQ = HM (câu a)
Do đó, t/g QMG = t/g HMG (c.g.c)
=> QG = HG (2 cạnh tương ứng) (đpcm)
c) t/g QMG = t/g HMG (câu b)
=> QGM = HGM (2 góc tương ứng)
Mà QGM + HGM = 180o
Nên QGM = HGM = 90o
=> QH _|_ OM (đpcm)
NV
9 tháng 5 2022
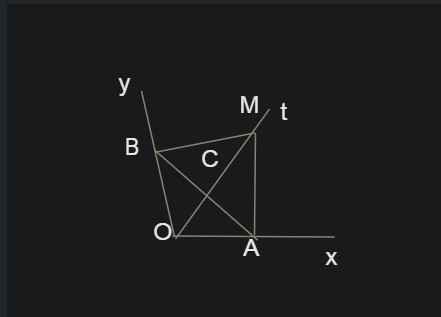
a) Xét tam giác vuông AMO và tam giác vuông BMO :
góc MOA = góc MOB (gt)
OM là cạnh chung
=>tam giác vuông AMO = tam giác vuông BMO (cạnh huyền + góc nhọn)
=> OA=OB ( 2 cạnh tương ứng)
b) theo a) ta có : tam giác AMO = tam giác BMO
=>góc AMO = góc BMO
=> MO là tia phân giác của góc AMB
c) gọi C là giao điểm của OM và AB
Xét tam giác OAC và tam giác OBC có:
góc AOC = góc BOC (gt)
OC là cạnh chung
OA = OB (theo a)
=>tam giác OAC = tam giác OBC
=> góc ACO = góc BCO
mà hai góc này kề bù
=> góc ACO = góc BCO = 90 độ
=> OM vuông góc với AB
23 tháng 12 2020
Sửa đề: Chứng minh OM⊥HQ
| GT | \(\widehat{xOy}< 90^0\) Ot là tia phân giác của \(\widehat{xOy}\) M∈Ot MH⊥Oy tại H MQ⊥Ox tại Q QH\(\cap\)Ot={G} |
| KL | a) MQ=MH b) GQ=GH c) QH⊥OM |
a) Xét ΔOHM vuông tại H và ΔOQM vuông tại Q có
OM chung
\(\widehat{HOM}=\widehat{QOM}\)(Ot là tia phân giác của \(\widehat{xOy}\), H∈Oy, Q∈Ox, M∈Ot)
Do đó: ΔOHM=ΔOQM(cạnh huyền-góc nhọn)
⇒MH=MQ(hai cạnh tương ứng)
b) Ta có: ΔOHM=ΔOQM(cmt)
nên OH=OQ(hai cạnh tương ứng)
Xét ΔOHQ có OH=OQ(cmt)
nên ΔOHQ cân tại O(Định nghĩa tam giác cân)
Ta có: ΔOHQ cân tại O(cmt)
mà OG là đường phân giác của ứng với cạnh đáy HQ
nen OG là đường trung tuyến ứng với cạnh HQ(Định lí tam giác cân)
⇒G là trung điểm của HQ
hay GH=GQ(đpcm)
c) Ta có: OH=OQ(cmt)
nên O nằm trên đường trung trực của HQ(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: GH=GQ(cmt)
nên G nằm trên đường trung trực của HQ(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra OG là đường trung trực của HQ
hay OG⊥HQ(đpcm)
câu a xét 2 tam giác bằng nhau em nhé