Cho ΔABC cân tại A. Trên tia đối của BC lấy điểm M, trên tia đối của CB lấy điểm N, sao cho BM=CN.
a) Cm: ΔABM=ΔACN
b) Kẻ BH vuông góc AM; CK vuông góc AN (H thuộc AM; K thuộc AN). Cm: AH=AK
c) Gọi O là giao điểm của BH và KC. ΔOBC là Δ gì? Vì sao?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABH và ΔACK có
AB=AC
\(\widehat{ABH}=\widehat{ACK}\)
BH=CK
Do đó: ΔABH=ΔACK
Suy ra: AH=AK
hay ΔAHK cân tại A
b: Xét ΔAMB vuông tại M và ΔANC vuông tại N có
AB=AC
\(\widehat{MAB}=\widehat{NAC}\)
Do đó: ΔAMB=ΔANC
Suy ra: AM=AN
hay ΔAMN cân tại A

a: XétΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
Suy ra AM=AN
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔAHB=ΔAKC
Suy ra: BH=CK

a: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
Suy ra: AM=AN
Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔAHB=ΔAKC
b: Xét ΔAMN có
AH/AM=AK/AN
nên HK//MN
hay KH//BC

a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
b: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó;ΔABM=ΔACN
Suy ra: \(\widehat{M}=\widehat{N}\)
Xét ΔEBM vuông tại E và ΔFCN vuông tại F có
BM=CN
\(\widehat{M}=\widehat{N}\)
Do đó: ΔEBM=ΔFCN
Suy ra: \(\widehat{EBM}=\widehat{FCN}\)
=>\(\widehat{IBC}=\widehat{ICB}\)
=>ΔIBC cân tại I
=>IB=IC
mà AB=AC
và HB=HC
nên A,H,I thẳng hàng

a) Ta có: \(\widehat{ABM}+\widehat{ABC}=180^0\)(hai góc kề bù)
\(\widehat{ACN}+\widehat{ACB}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)
nên \(\widehat{ABM}=\widehat{ACN}\)
Xét ΔABM và ΔACN có
AB=AC(ΔABC cân tại A)
\(\widehat{ABM}=\widehat{ACN}\)(cmt)
BM=CN(gt)
Do đó: ΔABM=ΔACN(c-g-c)
Suy ra: AM=AN(hai cạnh tương ứng)
Xét ΔAMN có AM=AN(cmt)
nên ΔAMN cân tại A(Định nghĩa tam giác cân)
b) Xét ΔHBM vuông tại H và ΔKCN vuông tại K có
BM=CN(gt)
\(\widehat{HMB}=\widehat{KNC}\)(hai góc ở đáy trong ΔAMN cân tại A)
Do đó: ΔHBM=ΔKCN(cạnh huyền-góc nhọn)
Suy ra: BH=CK(hai cạnh tương ứng)
c) Ta có: ΔHBM=ΔKCN(cmt)
nên HM=KN(hai cạnh tương ứng)
Ta có: AH+HM=AM(H nằm giữa A và M)
AK+KN=AN(K nằm giữa A và N)
mà AM=AN(cmt)
và HM=KN(cmt)
nên AH=AK(đpcm)
d) Ta có: ΔHBM=ΔKCN(cmt)
nên \(\widehat{HBM}=\widehat{KCN}\)(hai góc tương ứng)
mà \(\widehat{OBC}=\widehat{HBM}\)(hai góc đối đỉnh)
và \(\widehat{OCB}=\widehat{KCN}\)(hai góc đối đỉnh)
nên \(\widehat{OBC}=\widehat{OCB}\)
Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)(cmt)
nên ΔOBC cân tại O(Định lí đảo của tam giác cân)

Xét ΔBHM vuông tại H và ΔCKN vuông tại K có:
BM = CN (gt)
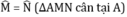
⇒ ΔBHM = ΔCKN (cạnh huyền – góc nhọn)
⇒ BH = CK (hai cạnh tương ứng)