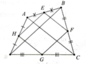
Cho tứ giác ABCD, các điểm E; F; G; H theo thứ tự chia trong các cạnh AB, BC, CD, DA theo tỉ lệ 1:2. CMR:
a) EG = FH
b) EG | FH
Vẽ hình hộ mik luôn nha,
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chứng minh EFGH là hình bình hành. Để EFGH là hình chữ nhật thì
Þ H E F ^ = 90 0 ⇒ H E ⊥ E F
Þ AC ^BD.

a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{\widehat{A}}{1}=\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{3}=\dfrac{\widehat{D}}{4}=\dfrac{360^0}{10}=36^0\)
Do đó: \(\widehat{A}=36^0;\widehat{B}=72^0;\widehat{C}=108^0;\widehat{D}=144^0\)
b: ta có: \(\widehat{B}+\widehat{C}=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên AB//CD

a: Xét ΔBAC có
E,F lần lượt là trung điểm của BA,BC
=>EF là đường trung bình
=>EF//AC và EF=AC/2
Xét ΔCDA có
G,H lần lượt là trung điểm của DC,DA
=>GH là đường trung bình
=>GH//AC và GH=AC/2
=>EF//GH và EF=GH
Xét tứ giác EFGH có
EF//GH
EF=GH
=>EFGH là hình bình hành
b: Để EFGH là hình chữ nhật thì HE vuông góc EF
=>AC vuông góc BD

Em tự vẽ hình nhé. Ý sau cô nói rõ yêu cầu hơn là chứng minh hình bình hành MNPQ có chu vi bằng tổng độ dài hai đường chéo của tứ giác ABCD.
Xét tứ giác EFMN có OF = ON; OE = OM nên nó là hình bình hành (Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Vậy thì MN // EF // AC và MN = EF = AC / 2 (Vì EF là đường trung bình tam giác BAC).
Hoàn toàn tương tự: QP // GH // AC và QP = GH = AC/2.
Vậy MNPQ là hình bình hành (Cặp cạnh đối song song và bằng nhau).
Khi đó ta có:
\(p_{MNPQ}=PQ+PN+NM+MQ=\left(PQ+MN\right)+\left(MQ+PN\right)=AC+BD.\)
Vậy ta đã chứng minh xong bài toán.

a: Xét ΔABD có
E là trung điểm của AB
H là trung điểm của AD
Do đó: EH là đường trung bình của ΔABD
Suy ra: EH//BD và \(EH=\dfrac{BD}{2}\left(1\right)\)
Xét ΔBCD có
F là trung điểm của BC
G là trung điểm của DC
Do đó: FG là đường trung bình của ΔBCD
Suy ra: FG//BD và \(FG=\dfrac{BD}{2}\left(2\right)\)
Từ (1) và (2) suy ra EH//GF và EH=GF
hay EHGF là hình bình hành

Xét ΔABD có
E là trung điểm của AB
H là trung điểm của AD
Do đó: EH là đường trung bình của ΔABD
Suy ra: EH//BD và \(EH=\dfrac{BD}{2}\left(1\right)\)
Xét ΔBCD có
F là trung điểm của BC
G là trung điểm của CD
Do đó: FG là đường trung bình của ΔBCD
Suy ra: FG//BD và \(FG=\dfrac{BD}{2}\left(2\right)\)
Từ (1) và (2) suy ra EH//FG và EH=FG
hay EHGF là hình bình hành

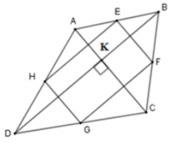
Vì E, F, G, H lần lượt là trung điểm các cạnh AB,BC,CD,DA nên EF, FG, GH, HE lần lượt là đường trung bình của tam giác ABC, BCD, ADC, ADB nên
EF//HG (cùng song song với AC)
HE//FG (cùng song song với BD)
Suy ra tứ giác EFGH là hình bình hành
Mà A C ⊥ B D (gt) ⇒ E F ⊥ F G
Suy ra EFGH là hình chữ nhật
Do đó S E F G H = H E . E F mà E F = 1 2 A C ; H E = 1 2 B D (tính chất đường trung bình)


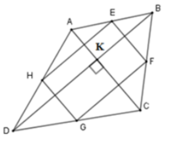
Vì E, F, G, H lần lượt là trung điểm các cạnh AB,BC,CD,DA nên EF, FG, GH, HE lần lượt là đường trung bình của tam giác ABC, BCD, ADC, ADB nên
EF//HG (cùng song song với AC)
HE//FG (cùng song song với BD)
Suy ra tứ giác EFGH là hình bình hành
Mà A C ⊥ B D (gt) ⇒ E F ⊥ F G
Suy ra EFGH là hình chữ nhật
Do đó S E F G H = H E . E F mà E F = 1 2 A C ; H E = 1 2 B D (tính chất đường trung bình)

Đáp án D
GỌI M,N THEO THỨ TỰ LÀ TRUNG ĐIỂM CỦA CF,DG
TA CÓ\(CM=\frac{1}{2};CF=\frac{1}{3};BC\Rightarrow\frac{BM}{BA}=\frac{1}{3}\Rightarrow\frac{BE}{BA}=\frac{BM}{BC}=\frac{1}{3}\)
=>EM//AC\(\Rightarrow\frac{EM}{AC}=\frac{BM}{BE}=\frac{2}{3}\Rightarrow EM=\frac{2}{3}AC\left(1\right)\)
TƯƠNG TỰ,TA CÓ:NF//BD\(\Rightarrow\frac{NF}{BD}=\frac{CF}{CB}=\frac{2}{3}\Rightarrow NF=\frac{2}{3}BD\left(2\right)\)
MÀ AC=BD(3) TỪ (1);(2);(3) SUY RA EM=NF(A)
TƯƠNG TỰ NHƯ TRÊN TA CÓ:MG//BD,NH//AC VÀ MG=NH=\(\frac{1}{3}AC\left(B\right)\)
MẶC KHÁC EM//AC;MG//BD VÀ \(AC\perp BD\Rightarrow EM\perp MG\Rightarrow\widehat{EMG}=90^0\left(4\right)\)
TƯƠNG TỰ TA CÓ:\(\widehat{FNH}=90^0\left(5\right)\)TỪ (4) VÀ (5) SUY RA \(\widehat{EMG}=\widehat{FNH}=90^0\left(C\right)\)
TỪ (A),(B),(C) SUY RA \(\Delta EMG=\Delta FNH\left(C.G.C\right)\Rightarrow EG=FH\)
B)GỌI GIAO ĐIỂM CỦA EG VÀ FH LÀ O;CỦA EM VÀ FH LÀ P;CỦA EM VÀ FN LÀ Q THÌ
\(\widehat{PQF}=90^0\Rightarrow\widehat{QPF}+\widehat{QFP}=90^0\)MÀ \(\widehat{QPF}=\widehat{OPE}\)(ĐỐI ĐỈNH),\(\widehat{OEP}=\widehat{QFP}\left(\Delta EMG=\Delta FNH\right)\)
\(\Rightarrow\widehat{EOP}=\widehat{PQF}=90^0\Rightarrow EO\perp OP\Rightarrow EG\perp FH\)