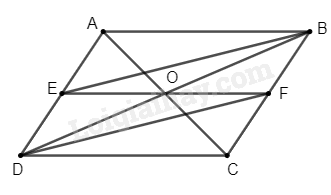
Cho hình bình hành ABCD. Gọi E; F và O lần lượt là trung điểm của AB; CD và BD. Gọi I và K là
điểm bất kì trên AD và BC.
a) Chứng minh AI song song CK. b) Chứng minh AE = FC.
c) Chứng minh A; O và C thẳng hàng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(AD = BC\); \(AD\) // \(BC\)
Mà \(E\), \(F\) là trung điểm của \(AD\), \(BC\) (gt)
Suy ra \(AE = ED = BF = FC\)
Xét tứ giác \(EBFD\) ta có:
\(ED = FB\) (cmt)
\(ED\) // \(BF\) (do \(AD\) // \(BC\))
Suy ra \(EDFB\) là hình bình hành
b) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(O\) là trung điểm của \(AC\) và \(BD\)
Mà \(DEBF\) là hình bình hành (gt)
Suy ra \(O\) cũng là trung điểm của \(EF\)
Suy ra \(E\), \(O\), \(F\) thẳng hàng

Xét tứ giác DEBF có
DE//BF
DE=BF
Do đó: DEBF là hình bình hành

a: Xét ΔMEA và ΔMCB có
góc EMA=góc CMB
MA=MB
góc MEA=góc MCB
=>ΔMEA=ΔMCB
=>ME=MC
=>M là trung điểm của CE
Xét tứ giác AEBC có
M là trung điểm chung của AB và EC
=>AEBC là hbh
b: Để AEBC là hình chữ nhật thì góc EAC=90 độ
=>góc DAC=90 độ
=>góc ACD+góc D=90 độ
mà góc ACD=1/2*góc D
nên góc D=2/3*90=60 độ
=>góc B=60 độ
góc BAD=góc BCD=180-60=120 độ

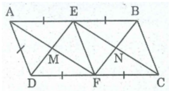
Ta có: Hình chữ nhật EMFN là hình thoi ⇒ ME = MF
ME = 1/2 DE (tính chất hình thoi)
MF = 1/2 AF (tính chất hình thoi)
Suy ra: DE = AF
⇒ Tứ giác AEFD là hình vuông (vì hình thoi có 2 đường chéo bằng nhau)
⇒ ∠ A = 90 0 ⇒ Hình bình hành ABCD là hình chữ nhật.
Ngược lại: ABCD là hình chữ nhật ⇒ ∠ A = 90 0
Hình thoi AEFD có ∠ A = 90 0 nên AEFD là hình vuông
⇒ AF = DE ⇒ ME = MF (tính chất hình vuông)
Hình chữ nhật EMFN là hình vuông (vì có 2 cạnh kề bằng nhau)
Vậy hình chữ nhật EMFN là hình vuông nếu ABCD là hình chữ nhật có AB = 2AD.

AEFD và BCFE có phải hình bình hành đâu bạn? Bạn coi lại đề.

Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành

a: Xét ΔADE vuông tại E và ΔCBF vuông tại F có
AD=CB
\(\widehat{ADE}=\widehat{CBF}\)
Do đó: ΔADE=ΔCBF
Suy ra: AE=CF
b: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành

a/
Ta có
AB = CD (cạnh đối hình bình hành)
AE = BE (gt); CF=DF (gt)
=> AE = BE = CF = DF
Xét tứ giác AEFD có
AB//CD (cạnh đối hình bình hành)
=> AE//DF mà AE = DF (cmt) => AEFD là hbh (tứ giác có cặp cạnh đối // và bằng nhau là hình bình hành)
Xét tứ giác AECF có
AB//CD (cạnh đối hbh)
=> AE//CF mà AE = CF => AECF là hình bình hành (lý do như trên)
b/
Do AEFD là hbh => EF=AD (cạnh đối hbh)
C/m tương tự như câu a ta cũng có BEDF là hbh => BF=DE (cạnh đối hbh)
C/m tương tự có AECF là hbh => AF=EC (cạnh đối hbh)

Lời giải:
a. $I\in AD, K\in CB$ mà $AD\parallel CB$ (tính chất hình bình hành)
$\Rightarrow AI\parallel CK$
b.
Do $E$ là trung điểm $AB$ nên $AE=\frac{1}{2}AB$
Do $F$ là trung điểm $CD$ nên $CF=\frac{1}{2}CD$
Mà $AB=CD$ (tính chất hbh)
$\Rightarrow AE=CF$
c.
Tính chất hbh phát biểu rằng 2 đường chéo cắt nhau tại trugn điểm mỗi đường
Do đó $AC$ cắt $BD$ tại trung điểm $BD$. Mà trung điểm của $BD$ là $O$ nên $A,O,C$ thẳng hàng
Hình vẽ:
