Cho hình thang ABCD ( AB//CD ) có AB = 3cm; CD = 5cm, chiều cao hình thang là h = 4cm. Tính diện tích hình thang ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
15 tháng 7 2017
Đúng(0)
Những câu hỏi liên quan
1
14 tháng 6 2021
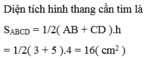
từ A hạ \(AE\perp DC\)
từ B hạ \(BF\perp DC\)
\(AB//CD=>AB//EF\)\(=>ABCD\) là hình chữ nhật
\(=>AB=EF=2cm\)
vì ABCD là hình thang cân\(=>\left\{{}\begin{matrix}AD=BC\\\angle\left(ADE\right)=\angle\left(BCF\right)\end{matrix}\right.\)
mà \(\angle\left(AED\right)=\angle\left(BFC\right)=90^o\)
\(=>\Delta ADE=\Delta BFC\left(ch.cgn\right)=>DE=FC=\dfrac{DC-EF}{2}=\dfrac{6-2}{2}=2cm\)
xét \(\Delta ADE\) vuông tại E có: \(AE=\sqrt{AD^2-ED^2}=\sqrt{3^2-2^2}=\sqrt{5}cm\)
\(=>S\left(ABCD\right)=\dfrac{\left(AB+CD\right)AE}{2}=\dfrac{\left(2+6\right)\sqrt{5}}{2}=4\sqrt{5}cm^2\)
DC
0
GH
1
21 tháng 9 2021
Kẻ BM//AD( \(M\in AD\))
Xét tứ giác ABMD có:
BM//AD(cách vẽ)
AB//DM( do AB//CD, \(M\in DC\))
=> Tứ giác ABMD là hình bình hành
=> AD=BM và AB=DM
Ta có: DM+MC=DC
=> AB+MC=DC
=> MC=DC-AB = 7-4=3cm
Xét tam giác BMC có:
BM + BC > MC( bất đẳng thức trong tam giác)
Mà BM=AD, MC= 4cm
=> AD+BC >4cm
CM
5 tháng 1 2020
Tương tự 1B. Tính được số đo của A ^ = 135 0 , B ^ = 90 0 , C ^ = 90 0 , D ^ = 45 0 , từ đó suy ra ABCD là hình thang vuông ⇒ B C ⊥ D C . Vận dụng nhận xét hình thang ABCH (AB//CH) có hai cạnh bên song song thì hai cạnh đáy bằng nhau, để tính được CH = 3cm, từ đó suy ra DH = 1cm.
Chứng minh được DAHD vuông cân tại H Þ AH = 1cm
Þ diện tích hình thang ABCD là 3,5cm2
10 tháng 8 2021
a: Xét hình thang ABCD(AB//CD có
\(\widehat{B}=\widehat{C}\)
nên ABCD là hình thang cân
3 tháng 4 2020
Kẻ BH//AD(H∈CD)BH//AD(H∈CD), kẻ BD
Ta có:
+) AB//CD (hình thang ABCD)
⇒B2ˆ=D1ˆ⇒B2^=D1^ ( 2 góc so le trong )
+) BH//AD (cách vẽ)
⇒D2ˆ=B1ˆ⇒D2^=B1^ ( 2 góc so le trong)
Xét ΔDABΔDAB và ΔBHDΔBHD, ta có:
B2ˆ=D1ˆ(cmt)B2^=D1^(cmt)
BD : chung
D2ˆ=B1ˆ(cmt)D2^=B1^(cmt)
⇒⇒ ΔDABΔDAB = ΔBHDΔBHD (gcg)
⇒AD=BH⇒AD=BH
mà AD=3cm(gt)AD=3cm(gt)
⇒BH=3cm⇒BH=3cm
+) ΔDABΔDAB = ΔBHDΔBHD (cmt)
⇒AB=DH⇒AB=DH
mà AB=4cm(gt)AB=4cm(gt)
⇒DH=4cm⇒DH=4cm
+) DH+HC=DC(H∈DC)DH+HC=DC(H∈DC)
⇒4+HC=8⇒4+HC=8
⇒HC=4cm⇒HC=4cm
Xét ΔBHC,ΔBHC, ta có:
52=32+4252=32+42
⇒BC2=BH2+HC2⇒BC2=BH2+HC2 (Định lý Py-ta-go)
⇒ΔBHC⇒ΔBHC vuông tại H
⇒H1ˆ=900⇒H1^=900
+) AD//BH
⇒ADHˆ=H1ˆ⇒ADH^=H1^ (2 góc động vị)
⇒ADHˆ=900⇒ADH^=900
⇒⇒ Hình thang ABCD là hình thang vuông