Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a+b)xét tg ABC có AF=FB( gt)
AE=EC( gt)
=> EF là dg tb tg ABC=> EF//BC=> EFBC là hình thang
Ta có tg Cân ABC=> B=C=(180o-A):2=52,5o
Ta có EF//BC => EFB+B=180( hai góc trong cùng phía bù nhau)
=> EFB=180-B=180-52,5=127,50
Hình thang EFBC có B=C( tg ABC cân tại A)
=> EFBC là htc => EFB=FEC
a) Áp dụng định lí Py-ta-go cho \(\Delta ABC\)vuông tại A ta có :
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow BC^2=5^2+12^2\)
\(\Leftrightarrow BC^2=169\)
\(\Leftrightarrow BC=13\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác ta có : \(AB.AC=BC.AH\)
\(\Leftrightarrow AH=\frac{5.12}{13}=\frac{60}{13}\left(cm\right)\)
b) Áp dụng hệ thức lượng ta có \(AB^2=BH.BC\Leftrightarrow BH=\frac{5^2}{13}=\frac{25}{13}\left(cm\right)\)
Do BE là tia phân giác \(\widehat{ABC}\)
\(\Rightarrow\frac{AE}{HE}=\frac{AB}{BH}=5\div\frac{25}{13}=\frac{13}{5}\)
Theo dãy tỉ số bằng nhau ta được :
\(\frac{AE}{13}=\frac{HE}{5}=\frac{AE+HE}{13+5}=\frac{AH}{18}=\frac{60}{13}\div18=\frac{10}{39}\)
\(\Rightarrow AE=\frac{10}{39}\times13=\frac{10}{3}\left(cm\right)\)
Mặt khác BF là tia phân giác \(\widehat{ABC}\)
\(\Rightarrow\frac{AF}{FC}=\frac{AB}{BC}=\frac{5}{13}\)
Theo dãy tỉ số bằng nhau ta được :
\(\frac{AF}{5}=\frac{FC}{13}=\frac{AF+FC}{5+13}=\frac{AC}{18}=\frac{2}{3}\)
\(\Rightarrow AF=\frac{2}{3}\times5=\frac{10}{3}\left(cm\right)\)
Xét \(\Delta AEF\)có \(AE=AF\left(=\frac{10}{3}cm\right)\)
\(\Rightarrow\Delta AEF\)cân tại A ( đpcm )
Vậy ...
Do tam giác ABC là tam giác cân nên AH là đường cao đồng thời là đường trung tuyến nên:
\(BH=CH=\dfrac{BC}{2}=\dfrac{5}{2}=2,5\left(cm\right)\)
Xét tam giác vuông ABH ta có:
\(sinB=\dfrac{BH}{AB}\)
\(\Rightarrow sin40^{o0}=\dfrac{2,5}{AB}\Rightarrow AB=\dfrac{2,5}{sin40^o}\approx4\left(cm\right)\)
Áp dụng định lý Py-ta-go vào tam giác đó ta có:
\(AB^2=BH^2+AH^2\)
\(\Rightarrow AH=\sqrt{AB^2-BH^2}=\sqrt{4^2-2,5^2}\approx3\left(cm\right)\)
Δ A B C cân tại A (gt) mà AM là trung tuyến nên AM cũng là đường cao của tam giác đó.
Vì AM là trung tuyến của Δ A B C nên M là trung điểm của BC
⇒ B M = B C 2 = 24 : 2 = 12 c m
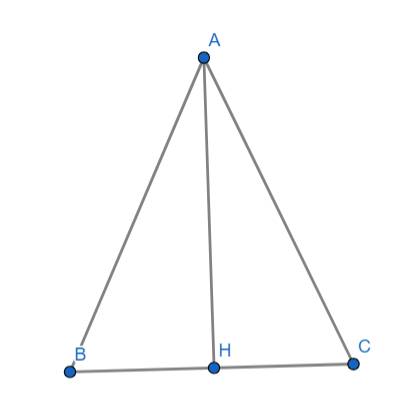
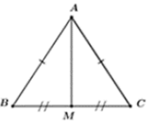
Hình:
Giải:
a) Ta có: \(AC< BC\left(5< 6\right)\)
\(\Leftrightarrow\widehat{ABC}< \widehat{BAC}\) (Quan hệ giữa cạnh và góc đối diện)
b) Xét tam giác ABD và tam giác ACD, có:
AD là cạnh chung
\(\widehat{ABD}=\widehat{ACD}\) (Tam giác ABC cân tại A)
\(\widehat{BAD}=\widehat{CAD}\) (AD là tia phân giác góc A)
\(\Rightarrow\Delta ABD=\Delta ACD\left(g.c.g\right)\)
c) Ta có tam giác ABC cân tại A có AD là phân giác
Suy ra AD đồng thời là đường trung tuyến của tam giác ABC
Mà AD cắt CE tại G
=> G là trọng tâm của tam giác ABC
=> CG là đường trung tuyến thứ ba của tam giác ABC
Măt khác CG cắt AB tại F
Nên F là trung điểm của AB
d) Không thể tính BG nếu đề bài chỉ cho dữ kiện như vậy, kết luận đề thiếu hoặc sai đề câu d, nếu đúng phải là tính AG hoặc GD.
Câu d đúng đề bạn ơi. Mk chỉ ko biết làm câu d thôi, chứ mấy câu khác mk biết òi