Cho tam giác ABC cân tại A. Tia phân giác góc B và C cắt AC và AB theo thứ tự ở D và E. Tính độ dài cạnh AB biết DE = 10cm; BC = 16cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


zì BD là phân giác cua góc B
\(=>\frac{AD}{DC}=\frac{AB}{DC}\)
CE là tia phân giác góc E
\(=>\frac{AE}{EB}=\frac{AC}{BC}=\frac{AB}{BC}\)
\(=>\frac{AD}{DC}=\frac{AE}{EB}=>DE//BC\)( định lý ta lét đào )
\(=>\widehat{EDB}=\widehat{DBC}\left(soletrong\right)\)
mà \(\widehat{DBC}=\widehat{EBD}\)( phân giác )
\(=>\widehat{EBD}=\widehat{EDB}=>\Delta EBD\left(cân\right)\)
=> ED=EB=10cm
theo định lý ta lét : do ED//BC
\(\frac{ED}{BC}=\frac{AE}{AB}=\frac{AB-EB}{AB}=>\frac{AB-10}{AB}=\frac{10}{16}=>AB=26.67\)

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=4^2+3^2=25\)
=>BC=5(cm)
b: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó:ΔBAD=ΔBED
c: Sửa đề: ΔBHC đều
Ta có: ΔBAD=ΔBED
=>BA=BE
Xét ΔBEH vuông tại E và ΔBAC vuông tại A có
BE=BA
\(\widehat{EBH}\) chung
Do đó: ΔBEH=ΔBAC
=>BH=BC
Xét ΔBHC có BH=BC và \(\widehat{HBC}=60^0\)
nên ΔBHC đều

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=4^2+3^2=25\)
=>BC=5(cm)
b: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó:ΔBAD=ΔBED
c: Sửa đề: ΔBHC đều
Ta có: ΔBAD=ΔBED
=>BA=BE
Xét ΔBEH vuông tại E và ΔBAC vuông tại A có
BE=BA
\(\widehat{EBH}\) chung
Do đó: ΔBEH=ΔBAC
=>BH=BC
Xét ΔBHC có BH=BC và \(\widehat{HBC}=60^0\)
nên ΔBHC đều

a, Xét \(\Delta ABC\)VUÔNG tại A
Áp dụng định lý pitago ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AB^2=BC^2-AC^2\)
\(\Rightarrow AB^2=10^2-6^2\)
\(\Rightarrow AB^2=100-36\)
\(\Rightarrow AB^2=64\)
\(\Rightarrow AB=\sqrt{64}=8\)
VẬY AB=8 cm
b, Xét \(\Delta ABD\)và \(\Delta HBD\)CÓ:
\(\widehat{BAD}=\widehat{BHD}=90độ\)
\(\widehat{ABD}=\widehat{HBD}\)(do BD là tia phân giác của \(\widehat{B}\))
BD là cạnh chung
\(\Rightarrow\Delta ABD=\Delta HBD\)(ch-gn)
\(\Rightarrow AD=HD\)(2 CẠNH TƯƠNG ỨNG)
c,Do \(\Delta ABD=\Delta HBD\left(câub\right)\)
\(\Rightarrow\widehat{BDA}=\widehat{BDH}\)(2 góc tương ứng)
lại có \(\widehat{ADK}=\widehat{HDC}\)(đối đỉnh)
\(\Rightarrow\widehat{BDA}+\widehat{ADK}=\widehat{BDH}+\widehat{HDC}\)
\(\Rightarrow\widehat{BDK}=\widehat{BDC}\)
Xét \(\Delta KBD\) VÀ \(\Delta CBD\)CÓ:
\(\widehat{ABD}=\widehat{CBD}\)(Do BD là tia phân giác của \(\widehat{B}\))
BD là cạnh chung
\(\widehat{BDK}=\widehat{BDC}\left(cmt\right)\)
Do đó \(\Delta KBD=\Delta CBD\left(g-c-g\right)\)
\(\Rightarrow BK=BC\)(2 CẠNH TƯƠNG ỨNG)
\(\Rightarrow\Delta KBC\) cân tại B

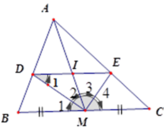
Vì DI = IE (cmt) nên MI là đường trung tuyến của tam giác MDE.
ΔMDE vuông (vì MD, ME là tia phân giác của góc kề bù) nên MI = DI = IE
Đặt DI = MI = x, ta có D I B M = A I A M (cmt) nên x 15 = 10 − x 10
Từ đó x = 6 suy ra DE = 12cm
Đáp án: D