Cho góc xOy = 600 , A thuộc Ox, B thuộc Oy ( A; B khác O ). CM: OA + OB = < 2AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 11 2017
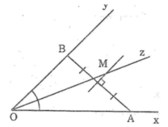
Vì điểm M nằm trong góc xOy và cách đều hai cạnh Ox và Oy nên M thuộc tia phân giác Oz của ∠(xOy).
Vì điểm M cách đều 2 điểm A và B nên M thuộc đường trung trực của AB.
Vậy M là giao điểm của đường trung trực của đoạn thẳng AB và tia phân giác Oz của ∠(xOy)
Do đó, có vô số điểm M thỏa mãn điều kiện trong câu a) khi OA = OB.
20 tháng 9 2019
Cm : a) Xét t/giác OAH và t/giác OBK
có: \(\widehat{OHA}=\widehat{OKB}=90^0\) (gt)
OA = OB (gt)
\(\widehat{O}\) :chung
=> t/giác OAH = t/giác OBK (ch - gn)
b) Xét t/giác OMH và t/giác OMK
có: \(\widehat{OHM}=\widehat{OKM}=90^0\) (gt)
OH = OK (vì t/giác OAH = t/giác OBK)
OM : chung
=> t/giác OMH = t/giác OMK (ch - cgv)
=> \(\widehat{O_1}=\widehat{O_2}\) (2 góc t/ứng)
=> OM là tia p/giác của góc xOy
20 tháng 7 2023
`a,` Gọi `a` giao `b` là `O'`.
Ta có: `hat(OAB) + hat(ABO') + hat(BO'A) + hat(AOB) = 360^o`
`<=> 90^o + 90^o + 90^o + hat(AO'B) =360^o`
`<=> hat(AO'B) = 90^o => a` vuông góc `b`.
`b,` Do `hat(xOy) = 90^o` nên `A, O, B` thẳng hàng.
Vì `hat(aAB) + hat(bBA) = 90^o + 90^o = 180^o` nên `a////b`.
19 tháng 2 2021
a) Xét ΔOAN vuông tại A và ΔOBN vuông tại B có
ON chung
\(\widehat{AON}=\widehat{BON}\)(ON là tia phân giác của \(\widehat{AOB}\))
Do đó: ΔOAN=ΔOBN(cạnh huyền-góc nhọn)
Suy ra: NA=NB(hai cạnh tương ứng)
b) Ta có: ΔOAN=ΔOBN(cmt)
nên OA=OB(hai cạnh tương ứng)
Xét ΔOAB có OA=OB(cmt)
nên ΔOAB cân tại O(Định nghĩa tam giác cân)
c) Xét ΔAND vuông tại A và ΔBNE vuông tại B có
NA=NB(cmt)
\(\widehat{AND}=\widehat{BNE}\)(hai góc đối đỉnh)
Do đó: ΔAND=ΔBNE(cạnh góc vuông-góc nhọn kề)
Suy ra: ND=NE(hai cạnh tương ứng)
d) Ta có: ΔAND=ΔBNE(cmt)
nên AD=BE(Hai cạnh tương ứng)
Ta có: OA+AD=OD(A nằm giữa O và D)
OB+BE=OE(B nằm giữa O và E)
mà OA=OB(cmt)
và AD=BE(cmt)
nên OD=OE
Ta có: OD=OE(cmt)
nên O nằm trên đường trung trực của DE(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: ND=NE(cmt)
nên N nằm trên đường trung trực của DE(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra ON là đường trung trực của DE
hay ON⊥DE(đpcm)
IG
27 tháng 2 2022
Cm: a) Xét t/giác OAB và t/giác OAC
có góc C = góc B = 900 (gt)
OA : chung
góc O1 = góc O2 (gt)
=> t/giác OAB = t/giác OAC (ch - gn)
=> AB = AC (hai cạnh tương ứng)
b) Áp dụng định lí Py - ta - go vào t/giác OAB vuông tại B, ta có :
OA2 = OB2 + AB2
=> AB2 = OA2 - OB2 = 52 - 42 = 25 - 16 = 9
=> AB = 3 (cm)