Cho hình chóp S . A B C D có đáy là hình thoi tâm O, cạnh bằng a 3 ; B A D ^ = 60 o ; SA vuông góc với mặt phẳng đáy, góc giữa đường thẳng SC và A B C D bằng 45 o . Gọi G là trọng tâm tam giác SCD. Khoảng cách giữa hai đường thẳng OG và AD bằng
A. a 17 17
B. a 5 5
C. 3 a 5 5
D. 3 a 17 17


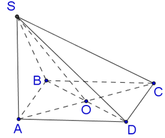
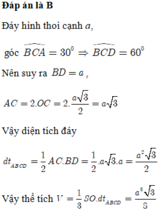

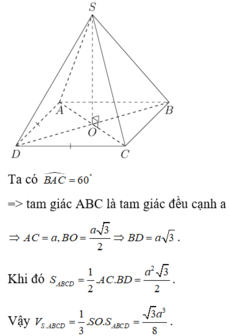


Chọn D