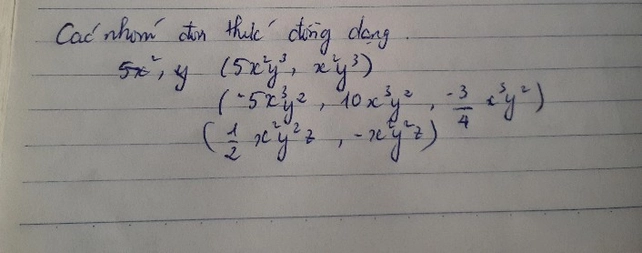Cho các đơn thức A = -2x^2y ; B = x^3y^4 ; C = 5x^3y^5 . Chứng minh rằng trong 3 đơn thức trên phải có ít nhất 1 đơn thức nhận giá trị âm hoặc bằng 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 7 2020
Bài làm:
a) Các đơn thức đồng dạng với nhau:
\(5x^2y\)và \(\frac{3}{2}x^2y\)
b) Ta có: \(B=-\frac{2}{3}xy^2.\left(-\frac{1}{2}x^2y\right)=\frac{1}{3}x^3y^3\)
=> Bậc đa thức B là 6
LL
3
30 tháng 5 2020
x = 1 và y = -1 thì mới ra nhé :V
\(A=3xy^2x^3\cdot\left(-x^2y^3\right)^2=3xy^2x^3\cdot x^4y^6=3\left(xx^3x^4\right)\left(y^2y^6\right)=3x^8y^8\)
Hệ số : 3
Biến : x8y8
Thay x = 1 ; y = -1 vào A ta được :
\(3\cdot1^8\cdot\left(-1\right)^8=3\cdot1\cdot1=3\)
Vậy giá trị của A = 3 khi x = 1 ; y = -1
\(B=\left(\frac{1}{2}x^2y^3\right)^2\cdot\left(-2x^3y\right)=\frac{1}{4}x^4y^6\cdot\left(-2x^3y\right)=\left(\frac{1}{4}\cdot-2\right)\left(x^4x^3\right)\left(y^6y\right)=\frac{-1}{2}x^7y^7\)
Hệ số : -1/2
Biến : x7y7
Thay x = 1 ; y = -1 vào B ta được : \(-\frac{1}{2}\cdot1^7\cdot\left(-1\right)^7=-\frac{1}{2}\cdot1\cdot\left(-1\right)=\frac{1}{2}\)
Vậy giá trị của B = 1/2 khi x = 1 ; y = -1