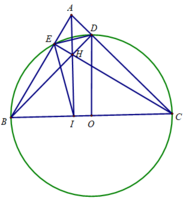
Cho tam giác ABC vuông tại A. Đường tròn tâm O đường kính AB cắt BC và OC lần lượt tại D và I. Gọi H là hình chiếu của A lên OC; AH cắt BC tại M
a) chứng minh tứ giác ACDH nội tiếp và góc CHD = góc ABC
b) chứng minh tam giác OHB = tam giác OBC và HM là tia phân giác góc BHD
c) Gọi K là trung điểm của BD.Chứng minh MD.BC = MB.CD và MB.MD=MK.MC