cho tam giác ACD vuông tại A (AC<AD) có M là trung điểm CD
a) Cho AC=12cm; AD=16cm. Tính CD và AM
b) Kẻ ME vuông AD tại E và MF vuông AC tại F là hình chủ nhật
d) Gọi B đối xứng với E qua A. chứng minh tứ giác ABFM là hình bình hành
e) Gọi K đối xứng với M qua E. Chứng minh tứ giác AMPK là hình thoi
f) chứng minh AM, FE và CK đồng quy

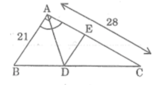
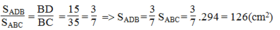

a,
áp dụng đl pytago:
\(CD^2=12^2+16^2=400\\ \Rightarrow CD=\sqrt{400}=20cm\)
\(AM=\dfrac{CD}{2}=\dfrac{20}{2}=10cm\)
b, xét tứ giác AFME có:
góc MFA= FAD=MEA=90\(^o\)
=> AFME là hcn
d,
xét tam giác ACD có đường tb FM(gt)
=>FM// và =AE
mà AE=AB và A nằm trên BE
=>FM// và =BA
vậy tứ giác ABMF là hình bình hành