Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a/ Xét \(\Delta ABC\) và \(\Delta HAC\) có :
\(\left\{{}\begin{matrix}\widehat{C}chung\\\widehat{BAC}=\widehat{AHC}=90^0\end{matrix}\right.\)
\(\Leftrightarrow\Delta ABC\sim HAC\left(g-g\right)\)
b/ \(BC=\sqrt{AB^2+AC^2}=10cm\)
\(AH.BC=AB.AC\Leftrightarrow AH=\dfrac{AB.AC}{BC}=4,8cm\)
c/ \(\Delta HEA\sim\Delta CEH\left(g-g\right)\)
\(\Leftrightarrow\dfrac{HE}{CE}=\dfrac{EA}{HE}\Leftrightarrow HE^2=EA.EC\left(đpcm\right)\)
a) Xét ΔHAC và ΔABC có:
∠(ACH ) là góc chung
∠(BAC)= ∠(AHC) = 90o
⇒ ΔHAC ∼ ΔABC (g.g)
b) Xét ΔHAD và ΔBAH có:
∠(DAH ) là góc chung
∠(ADH) = ∠(AHB) = 90o
⇒ ΔHAD ∼ ΔBAH (g.g)
c) Tứ giác ADHE có 3 góc vuông ⇒ ADHE là hình chữ nhật.
⇒ ΔADH= ΔAEH ( c.c.c) ⇒ ∠(DHA)= ∠(DEA)
Mặt khác: ΔHAD ∼ ΔBAH ⇒ ∠(DHA)= ∠(BAH)
∠(DEA)= ∠(BAH)
Xét ΔEAD và ΔBAC có:
∠(DEA)= ∠(BAH)
∠(DAE ) là góc chung
ΔEAD ∼ ΔBAC (g.g)
d) ΔEAD ∼ ΔBAC
ΔABC vuông tại A, theo định lí Pytago:
Theo b, ta có:
a:BC=căn 6^2+8^2=10cm
Xét ΔABC có AD là phân giác
nên BD/DC=AB/AC
=>BD/DC=3/4
=>BD/3=CD/4=(BD+CD)/(3+4)=10/7
=>BD=30/7cm
b: Xét ΔCED vuông tại E và ΔCAB vuông tại A có
góc C chung
=>ΔCED đồng dạng với ΔCAB
=>S CED/S CAB=(CD/CB)^2=(4/7)^2=16/49
Bạn tự vẽ hình nhé
a)
Áp dụng định lý Py-ta-go vào \(\Delta ABC:\)
\(BC^2=AB^2+AC^2\\ \Rightarrow BC^2=8^2+6^2\\ \Rightarrow BC^2=64+36\\ \Rightarrow BC^2=100\\ \Rightarrow BC=10\left(cm\right)\)
b)
Xét \(\Delta BGC\) và \(\Delta DGC\) có:
\(AB=AD\left(GT\right)\\ AG:chung\\ \widehat{BAC}=\widehat{DAC}\left(=90^o\right)\)
\(\Rightarrow\Delta BGC=\Delta DGC\left(c-g-c\right)\)
c)
Xét \(\Delta BCD\) có:
\(AB=AD\left(GT\right)\\ \dfrac{AG}{DG}=\dfrac{2}{6}=\dfrac{1}{3}\Rightarrow\dfrac{CG}{AC}=1-\dfrac{1}{3}=\dfrac{2}{3}\)
=> G là trọng tâm của \(\Delta BCD\)
=> DG là đường trung tuyến của \(\Delta BCD\) ứng với cạnh BC
Hay DG đi qua trung điểm BC
D A C B E M F y G 1 2 1 2
VẼ By là tia phân giác của \(\widehat{ABC}\)CẮT AC TẠI G
A) XÉT \(\Delta BAG\)VÀ \(\Delta BEG\)CÓ
\(\widehat{BAG}=\widehat{BEG}=90^o\)
BG LÀ CẠNH CHUNG
\(\widehat{B_1}=\widehat{B_2}\)( LẬP LUẬN)
=>\(\Delta BAG\)=\(\Delta BEG\)( CH-GN)
=>BA = BE
\(\Rightarrow\Delta ABE\)CÂN TẠI B ( ĐPCM)
VÌ \(\Delta BAG\)=\(\Delta BEG\)(CMT)
=> AG = GE
XÉT \(\Delta AGD\)VÀ \(\Delta EGC\)CÓ
\(\widehat{G_1}=\widehat{G_2}\)( ĐỐI ĐỈNH )
AG = GE ( CMT )
\(\widehat{DAG}=\widehat{CEG}=90^o\)
=>\(\Delta AGD\)=\(\Delta EGC\)( G-C-G )
=> AD = EC
TA CÓ
\(BA+AD=BD\)
\(BE+EC=BC\)
MÀ AD = EC(CMT) VÀ \(BA=BE\)(CMT)
=>\(BD=BC\)
=> \(\Delta BDC\)CÂN TẠI B
XÉT \(\Delta BDC\)CÂN TẠI B
\(\Rightarrow\widehat{BCD}=\frac{180^o-\widehat{B}}{2}\left(1\right)\)
XÉT \(\Delta BAE\)CÂN TẠI B
\(\Rightarrow\widehat{BEA}=\frac{180^o-\widehat{B}}{2}\left(2\right)\)
TỪ (1) VÀ (2)
\(\Rightarrow\widehat{BCD}=\widehat{BEA}\)
MÀ HAI GÓC NÀY Ở VỊ TRÍ ĐỒNG VỊ BẰNG NHAU
=>\(AE//CD\)(ĐPCM)
b) vì AE // CD HAY AF // CD \(\Rightarrow\widehat{FAC}=\widehat{DCA}\)( SO LE TROG )
XÉT \(\Delta FAM\)VÀ \(\Delta DCM\)CÓ \(\widehat{FAC}=\widehat{DCA}\)HAY\(\widehat{FAM}=\widehat{DCM};AM=CM\left(GT\right);\widehat{AMF}=\widehat{CMF}\left(DD\right)\)
=>\(\Delta FAM\)=\(\Delta DCM\)(G-C-G)
\(\Rightarrow FM=DM\)
XÉT\(\Delta ADM\)VÀ \(\Delta CFM\)CÓ \(AM=CM\left(GT\right);\widehat{AMD}=\widehat{CMF}\left(GT\right);FM=DM\left(CMT\right)\)
=>\(\Delta ADM\)=\(\Delta CFM\)(C-G-C)
\(\Rightarrow\widehat{DAM}=\widehat{FCM}=90^o\)
mà\(\widehat{FCM}=90^o\)
\(\Rightarrow CF\perp AC\left(ĐPCM\right)\)
a) Áp dụng Định lý Pythagoras cho tam giác vuông ABC, ta được:
AB2+AC2=32+62=45=BC2=>BC=\(\sqrt{45}\)cm
b) Xét \(\Delta\)BAD và \(\Delta\)EAD:
AE=AB(Do cùng bằng 3 cm)
BAD=EAD
AD chung
=>\(\Delta\)BAD=\(\Delta\)EAD(c-g-c)
c) Xét \(\Delta\)ABC và \(\Delta\)AEM:
A chung
AB=AE
ABC=AEM( Suy ra trực tiếp từ câu b)
=>\(\Delta\)ABC=\(\Delta\)AEM=>AC=AM=>\(\Delta\)CAM vuông cân tại A
d) Áp dụng Định lý Pythagoras cho tam giác vuông CAM, ta được:
AC2+AM2=MC2=>2.AC2=MC2( Do \(\Delta\)CAM vuông cân tại A)
Lại có:BC2=AC2+AB2
Do: AC>AB(gt)
Nên:MC>BC
Mặt khác:\(\Delta\)ABC=\(\Delta\)AEM(chứng minh trên)=>BC=ME
Suy ra MC>ME
a)áp dụng định lý pitago ta có BC^2=AB^2+AB^2=8^2+6^2=100
=>BC=10
b ) Ta có AB = AD ( gt )
=> CA là đường trung tuyến của BD
CA vuông góc với BD ( t/g ABC vuông tại A )
=> Ca là đường cao của BD
mà CA là đường trung tuyến của BD ( chứng minh trên )
t/g BCD cân tại C
=> CA cũng là p/g của t/g ABC
=> góc BCA = góc DCA
BC = CD ( t/g BCD cân tại C )
EC : cạnh chung
suy ra t/g BEC = t/g DEC ( c - g - c )
c ) Trên trung tuyến CA có CE/AC = 6-2/6 = 2/3
ba đường trung tuyến của t/g BCD đồng quy tại E
=> DE là đường trung tuyến của BC
=> DE đi qua trung điểm BC
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10cm
Áp dụng hệ thức lượng trong tam giác vuông ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB\cdot AC=AH\cdot BC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=4.8\left(cm\right)\\BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b:
Áp dụng hệ thức lượng trong tam giác vuông ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông ΔABH vuông tại A có HD là đường cao ứng với cạnh huyền BA, ta được:
\(AD\cdot AB=AH^2\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(AE\cdot AC=AD\cdot AB\)
hay \(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)
Xét ΔAED vuông tại A và ΔABC vuông tại A có
\(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)
Do đó: ΔAED\(\sim\)ΔABC
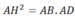
A B C H D E
a) AD là p/g của ΔABC => \(\dfrac{AB}{BD}=\dfrac{AC}{CD}\)
Áp dụng tính chất của dãy tỉ số bằng nhau :
\(\dfrac{AB}{BD}=\dfrac{AC}{CD}=\dfrac{AB+AC}{BD+CD}=\dfrac{6+8}{BC}=\dfrac{14}{10}=\dfrac{7}{5}\)
\(\Rightarrow BD=\dfrac{5AB}{7}=\dfrac{5.6}{7}=\dfrac{30}{7}\left(cm\right)\)
\(CD=\dfrac{5AC}{7}=\dfrac{5.8}{7}=\dfrac{40}{7}\left(cm\right)\)
b) Xét ΔABH và ΔCBA :
góc B chung
góc AHB = góc CAB (= 90o)
Do đó ΔABH ∼ ΔCBA (g.g)
=> \(\dfrac{AB}{CB}=\dfrac{BH}{BA}\)
=> AB2 = BH.CB
c) AB \(\perp\) AC
CE \(\perp\) AC
Nên AB // CE
=> góc ABD = góc ECD
Xét ΔABD và ΔECD :
góc ABD = góc ECD
góc BDA = góc CDE (đối đỉnh)
Nên ΔABD ∼ ΔECD (g.g)