Cho tam giác ABC vuông cân tại A. Các diểm D, E theo thứ tự di chuyển trên cạnh AB; AC sao cho Bd =AE. Xác định vị trí D;E sao cho;
a] DE có độ dài nhỏ nhất
b] Tứ giác BDEC có diện tích nhỏ nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 4 2018
Tương tự 2A.
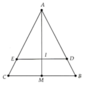
Cho D º B, E º C Þ Vị trí điểm I.
CHo D º A, E º A Þ Vị trí điểm I.
Kết luận: I thuộc trung trực của BC.
18 tháng 8 2017
a)
Đặt AB=AC=a (không đổi); BD=AE=b (0<x<a)
Áp dụng định lý Pi-ta go với \(\Delta ADE\) vuông tại A ta có:
\(DE^2=AD^2+AE^2=\left(a-x\right)^2+a^2=2x^2-2ax+a^2\)\(=2\left(x^2-ax\right)-a^2\)
\(=2\left(x-\frac{a^2}{4}\right)^2+\frac{a^2}{2}\ge\frac{a^2}{2}\)
Ta có DE nhỏ nhất \(\Leftrightarrow\)\(DE^2\) nhỏ nhất\(\Leftrightarrow x=\frac{a}{2}\)
\(\Leftrightarrow BD=AE=\frac{a}{2}\Leftrightarrow D,E\) là trung điểm của AB;AC.
Vậy D;E phải là trung điểm của AB;AC thì DE có độ dài nhỏ nhất.
b)
Ta có:\(S_{ADE}=\frac{1}{2}.AD.AE=\frac{1}{2}.AD.BD\)\(=\frac{1}{2}AD\left(AB-AD\right)=\frac{1}{2}\left(AD^2-AB.AD\right)\)
\(=-\frac{1}{2}\left(AD^2-2\frac{AB}{2}.AD+\frac{AB^2}{4}\right)+\frac{AB^2}{8}\)\(=-\frac{1}{2}\left(AD-\frac{AB}{4}\right)^2+\frac{AB}{2}\le\frac{AB^2}{8}\)
Vậy \(S_{BDEC}=S_{ABC}-S_{ADE}\ge\frac{AB^2}{2}-\frac{AB^2}{8}=\frac{3}{8}AB^2\) không đổi.
Do đó: \(min_{S_{BDEC}}=\frac{3}{8}AB^2\) khi D;E lần lượt là trung điểm của AB;AC.