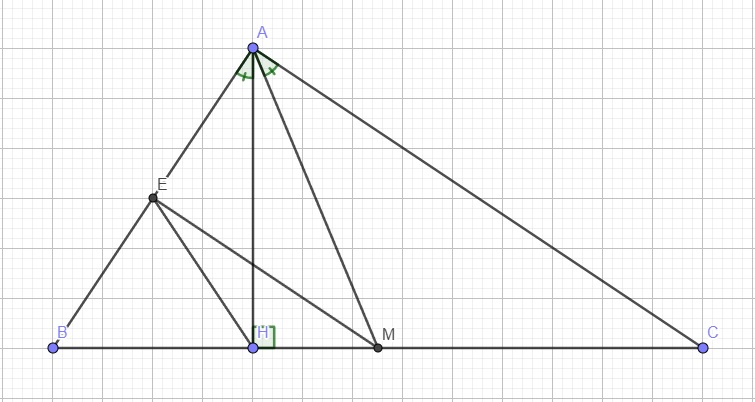
cho tam giac ABC có góc BAC nhỏ hơn 90 độ đường cao AH . gọi E ; F lần lượt là điểm đối xứng của H qua AB ; AC . đường thẳng EF cắt AB ; AC lần lượt tại M , N . chứng minh rằng : AE=AF , HA là tia phân giác của góc MHN , CM song song với EH ; BN song song với Fh
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 1 2024
a.
Do E là trung điểm AB, M là trung điểm BC
\(\Rightarrow\) EM là đường trung bình tam giác ABC
\(\Rightarrow EM||AC\)
\(\Rightarrow\widehat{MAC}=\widehat{AME}\) (so le trong) (1)
Trong tam giác vuông AHB, HE là trung tuyến ứng với cạnh huyền
\(\Rightarrow HE=\dfrac{1}{2}AB=AE\) \(\Rightarrow\Delta AHE\) cân tại E
\(\Rightarrow\widehat{AHE}=\widehat{BAH}\) (2)
Mà \(\widehat{BAH}=\widehat{MAC}\) (giả thiết) (3)
(1);(2);(3) \(\Rightarrow\widehat{AME}=\widehat{AHE}\)
\(\Rightarrow AMHE\) nội tiếp (2 góc bằng nhau cùng chắn AE)
\(\Rightarrow\) 4 điểm A, E, M, H cùng thuộc 1 đường tròn
b.
Theo cmt AMHE nội tiếp \(\Rightarrow\widehat{AEM}=\widehat{AHM}=90^0\) (cùng chắn AM)
\(\Rightarrow EM\perp AB\)
Mà \(EM||AC\)
\(\Rightarrow AB\perp AC\)
\(\Rightarrow\widehat{BAC}=90^0\)
2 tháng 4 2017
A B C H I M E
1) Do \(\Delta BAE\)có \(AB=AE\Rightarrow\Delta BAE\)cân vuông tại A
Mà \(AM\)là đường phân giác của \(\Delta BAE\)(hay\(\Delta ABC\))
\(\Rightarrow AM\)đồng thời là đường cao của \(\Delta BAE\Rightarrow\widehat{AMB}=\widehat{AME}=90^0\)
Ta có: \(\widehat{BAM}=\widehat{EAM}=\frac{\widehat{BAE}}{2}=45^0\left(1\right)\).Mà \(\Delta BAE\)vuông cân tại A\(\Rightarrow\widehat{ABM}=\widehat{AEM}=\frac{180^0-\widehat{BAE}}{2}=45^0\left(2\right)\)
Từ (1) và (2)\(\Rightarrow\Delta ABM\)vuông cân (đpcm)
2) Vì \(\Delta ABC\)có \(\widehat{BAC}=90^0\Rightarrow\widehat{ABC}+\widehat{ACB}=180^0-\widehat{BAC}=90^0\left(3\right)\)
Vì H là đường cao của \(\Delta ABC\Rightarrow\widehat{AHC}=90^0\Rightarrow\widehat{HAC}+\widehat{ACH}=180^0-\widehat{AHC}=90^0\)(Hay \(\widehat{HAC}+\widehat{ACB}=90^0\))\(\left(4\right)\)
Từ (3) và (4)\(\Rightarrow\widehat{ABC}=\widehat{HAC}=90^0-\widehat{ACB}\)(Hay \(\widehat{ABH}=\widehat{IAE}\))
Xét \(\Delta ABH\)và\(\Delta EAI\)có:\(\hept{\begin{cases}\widehat{AHB}=\widehat{EIA}=90^0\\AB=AE\\\widehat{ABH}=\widehat{EAI}\end{cases}}\Rightarrow\Delta ABH=\Delta EAI\)(cạnh huyền góc nhọn)
\(\Rightarrow IE=AH\)(Đpcm)