cho tam giác ABC có góc A= 120o ; AB=6cm
Tính góc A;C ; cạnh AC ; BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho tam giác ABC có Â = 120o, cạnh b = 8cm và c = 5cm. Tính cạnh a, các góc B̂, Ĉ của tam giác đó.

+ a2 = b2 + c2 - 2.bc.cosA = 82 + 52 – 2.5.8.cos120º = 129
⇒ a = √129 cm
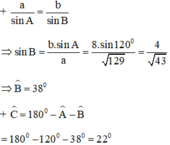



Hai tam giác vuông ABO (góc B = 90º) và ACO (góc C = 90º) có :

⇒ ΔABO = ΔACO (cạnh huyền – góc nhọn)
⇒ AB = AC (hai cạnh tương ứng) ⇒ ΔABC cân.
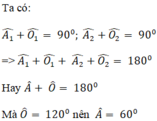
Tam giác cân ABC có góc A = 60º nên là tam giác đều.

Gọi I là giao điểm của AB và DC
△ADC△ADC và △ABE△ABE có:
AD=ABAD=AB
ˆDAC=600+ˆBAC=ˆBAEDAC^=600+BAC^=BAE^
AC=AEAC=AE
Nên △ADC=△ABE△ADC=△ABE (c.g.c) do đó ˆIDA=ˆABMIDA^=ABM^
Xét △ADI△ADI và △MIB△MIB có
ˆIDA=ˆABMIDA^=ABM^
ˆDIA=ˆMIBDIA^=MIB^ (đối đỉnh)
Nên ˆBMI=ˆIAD=600BMI^=IAD^=600
Vậy ˆBMC=1800−ˆBMI=1200BMC^=1800−BMI^=1200
Gọi N thuộc tia đối của ME sao cho MN=MDMN=MD thì △MND△MND đều do cóMN=MDMN=MD và ˆBMI=600BMI^=600
Xét △ADM△ADM và △DBN△DBN có:
AD=BDAD=BD
ˆADM=ˆBDN=600−ˆBDMADM^=BDN^=600−BDM^
DM=DNDM=DN
Nên △ADM△ADM và △BDN△BDN (c.g.c) do đó ˆAMD=ˆBND=600AMD^=BND^=600
Vậy ˆAMB=ˆAMD+ˆDMB=1200AMB^=AMD^+DMB^=1200

Ta có: OA là tia phân giác của \(\widehat{xOy}\)(gt)
nên \(\widehat{xOA}=\widehat{yOA}=\dfrac{\widehat{xOy}}{2}=\dfrac{120^0}{2}=60^0\)
hay \(\left\{{}\begin{matrix}\widehat{BOA}=60^0\\\widehat{COA}=60^0\end{matrix}\right.\)
Ta có: ΔAOC vuông tại C(AC\(\perp\)Oy tại C)
nên \(\widehat{CAO}+\widehat{COA}=90^0\)(hai góc nhọn phụ nhau)
hay \(\widehat{CAO}=30^0\)
Ta có: ΔAOB vuông tại B(AB\(\perp Ox\) tại B)
nên \(\widehat{BAO}+\widehat{BOA}=90^0\)(hai góc nhọn phụ nhau)
hay \(\widehat{BAO}=30^0\)
Ta có: \(\widehat{CAB}=\widehat{CAO}+\widehat{BAO}\)(tia AO nằm giữa hai tia AB,AC)
\(\Leftrightarrow\widehat{CAB}=30^0+30^0\)
hay \(\widehat{CAB}=60^0\)
Xét ΔAOC vuông tại C và ΔAOB vuông tại B có
AO chung
\(\widehat{CAO}=\widehat{BAO}\left(=30^0\right)\)
Do đó: ΔAOC=ΔAOB(cạnh huyền-góc nhọn)
hay AC=AB(hai cạnh tương ứng)
Xét ΔABC có AB=AC(cmt)
nên ΔABC cân tại A(Định nghĩa tam giác cân)
Xét ΔABC cân tại A có \(\widehat{BAC}=60^0\)(cmt)
nên ΔABC đều(Dấu hiệu nhận biết tam giác đều)

Trong tam giác BIC có ∠(BIC) + ∠(IBC) + ∠(ICB) = 180o ⇒ (IBC) + (ICB) = 60o
∠(ABC) + ∠(ACB) = 2∠(IBC) + 2∠(ICB) = 2(∠(IBC) + ∠(ICB) ) = 2.60o = 120o
Có ∠A = 180o - 120o = 60o. Chọn A

Phương pháp:
Sử dụng ![]()
Thể tích khối chóp V = 1 3 h.S với h là chiều cao hình chóp và S là diện tích đáy.
Cách giải:
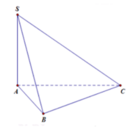
Diện tích đáy SABC = 1 2 AB. AC. sin BAC
![]()
Thể tích khối chóp
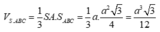
Chọn B.