Cho tam giác ABC vuông tại B. Giải tam giác ABC biết rằng:
b) cotC = \(\dfrac{1}{\sqrt{3}}\); AB = 5cm
c) AB = 8, BC = 15
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TM
20 tháng 7 2023
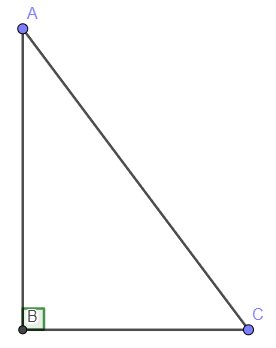
a, \(sin\left(A\right)=\dfrac{BC}{AC}\Leftrightarrow sin\left(40^o\right)=\dfrac{BC}{8}\Leftrightarrow BC\approx5,14\left(cm\right)\)
\(cos\left(A\right)=\dfrac{AB}{AC}\Leftrightarrow cos\left(40^o\right)=\dfrac{AB}{8}\Leftrightarrow AB\approx6,12\left(cm\right)\)
b,
\(cotg\left(C\right)=\dfrac{BC}{AB}\Leftrightarrow\dfrac{1}{\sqrt{3}}=\dfrac{BC}{5}\Leftrightarrow BC=\dfrac{5\sqrt{3}}{3}\left(cm\right)\)
\(AC^2=AB^2+BC^2\Leftrightarrow AC=\sqrt{AB^2+BC^2}=\sqrt{5^2+\left(\dfrac{5\sqrt{3}}{3}\right)^2}=\dfrac{10\sqrt{3}}{3}\left(cm\right)\)
KF
1
21 tháng 1 2022
Với có và
Gọi là trung điểm của
Mà có
( định lý)
cân tại
Mà
đều
29 tháng 11 2023
Ta có \(AC^2=CH.BC=AB.BC\)
Mà \(BC^2=AB^2+AC^2\) \(=AB^2+AB.BC\)
\(\Leftrightarrow AB^2+AB.BC-BC^2=0\)
\(\Leftrightarrow\left(\dfrac{AB}{BC}\right)^2+\dfrac{AB}{BC}-1=0\)
\(\Leftrightarrow\dfrac{AB}{BC}=\dfrac{-1+\sqrt{5}}{2}\) (loại TH \(\dfrac{AB}{BC}=\dfrac{-1-\sqrt{5}}{2}< 0\))
\(\Leftrightarrow\cos B=\dfrac{\sqrt{5}-1}{2}\), đpcm.
14 tháng 12 2023
a: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=5^2+12^2=169\)
=>\(BC=\sqrt{169}=13\left(cm\right)\)
Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{5}{13}\)
nên \(\widehat{B}\simeq23^0\)
Ta có: ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{C}\simeq90^0-23^0=67^0\)
b: Ta có: ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{C}=90^0-40^0=50^0\)
Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}\)
=>\(BC=\dfrac{AC}{sinB}=\dfrac{5}{sin40}\simeq7,78\left(cm\right)\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AB^2=BC^2-AC^2\)
=>\(AB\simeq\sqrt{7,78^2-5^2}\simeq5,96\left(cm\right)\)
AH
Akai Haruma
Giáo viên
17 tháng 6 2021
a.
Áp dụng hệ thức lượt trong tam giác vuông ta có:
$\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}$
$\Leftrightarrow \frac{1}{AC^2}=\frac{1}{AH^2}-\frac{1}{AB^2}=\frac{1}{3a^2}$
$\Rightarrow AC=\sqrt{3}a$
$BC=\sqrt{AB^2+AC^2}=\sqrt{a^2+3a^2}=2a$
b.
$HB=\frac{BC}{4}$ thì $HC=\frac{3}{4}BC$
$\Rightarrow \frac{HB}{HC}=\frac{1}{3}$
Áp dụng hệ thức lượt trong tam giác vuông:
$AB^2=BH.BC; AC^2=CH.BC$
$\Rightarrow \frac{AB}{AC}=\sqrt{\frac{BH}{CH}}=\frac{\sqrt{3}}{3}$
Áp dụng định lý Pitago:
$4a^2=BC^2=AB^2+AC^2=(\frac{\sqrt{3}}{3}.AC)^2+AC^2$
$\Rightarrow AC=\sqrt{3}a$
$\Rightarrow AB=a$
AH
Akai Haruma
Giáo viên
17 tháng 6 2021
c.
Áp dụng hệ thức lượt trong tam giác vuông:
$AB^2=BH.BC$
$\Leftrightarrow AB^2=BH(BH+CH)$
$\Leftrightarrow a^2=BH(BH+\frac{3}{2}a)$
$\Leftrightarrow BH^2+\frac{3}{2}aBH-a^2=0$
$\Leftrightarrow (BH-\frac{a}{2})(BH+2a)=0$
$\Rightarrow BH=\frac{a}{2}$
$BC=BH+CH=2a$
$AC=\sqrt{BC^2-AB^2}=\sqrt{3}a$
d. Tương tự phần a.
a) Để giải tam giác ABC, chúng ta cần biết thêm một thông tin khác về tam giác, ví dụ như độ dài cạnh AC hoặc giá trị của một góc trong tam giác. Với thông tin hiện tại, không đủ để giải tam giác ABC.
b) Từ công thức cotC = AB/BC, và AB = 5cm, ta có:
cotC = 5/BC = 1/3
Vậy, cotC = 1/3.
c) Từ định lý Pythagoras trong tam giác vuông, ta có:
AB^2 + BC^2 = AC^2
8^2 + 15^2 = AC^2
64 + 225 = AC^2
289 = AC^2
AC = √289
AC = 17 cm
Vậy, độ dài cạnh AC của tam giác ABC là 17cm