Tìm a,b,c là số tự nhiên thỏa mãn: a nhỏ nhất và 7a2 - 9b2 + 29=0 ; 9b2 - 11c2 - 25 = 0.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


7a2 - 9b2 + 29 = 0 9b2 - 11c2 - 25 = 0
vậy 7a2 - 9b2 = - 29 9b2 - 11c2 = 25
7 a2 kém 9 b2 29 đơn vị . suy ra b > c
đây là hơn : 9 - 7 = 2 ( đơn vị )
vậy không thể chia , suy ra a < b
ta ghép hai biểu thức lại : 7a2 - 9b2 + 29 = 9b2 - 11c2 - 25 = 0
một bên biểu thức là - 9b2 , còn 1 bên là + 9b2
vậy bỏ hai bên cùng 1 phép vẫn được kết quả cũ
suy ra a bé nhất = 1


Ta có:
\(\frac{a}{b}=\frac{14}{22}=\frac{14k}{22k}=>a=14k,b=22k=>M=a+b=14k+22k=36k\)
\(\frac{c}{d}=\frac{11}{13}=\frac{11m}{13m}=>c=11m,d=13m=>M=c+d=11m+13m=24m\)
\(\frac{e}{f}=\frac{13}{17}=\frac{13n}{17n}=>e=13n,f=17n=>M=e+f=13n+17n=30n\)
=>M=36k=24m=30n
=>M chia hết cho 36,24,30
Ta thấy: ƯCLN(36,24,30)=360
=>M chia hết cho 360
=>M=360h
mà M là số bé nhất có 4 chữ số=>h bé nhất
=>999<360h
=>2<h
mà h bé nhất
=>h=3
=>M=3.360=1080
Vậy M=1080
$\frac{a}{b}=\frac{14}{22}=\frac{14k}{22k}=>a=14k,b=22k=>M=a+b=14k+22k=36k$

a, a = BCNN(15;115) = 345
b, a – 1 ∈ BC(35;52) và 999 < a – 1 < 1999
Ta có BCNN(35;52) = 35.52 = 1820
Suy ra a – 1 ∈ {0;1820;3640;...}
Vì 999 < a – 1 < 1999 nên a – 1 = 1820
a = 1821
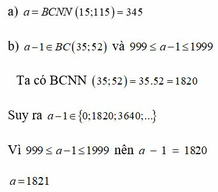
kết quả bằng 75,75