Viết phương trình của Parabol (P) biết rằng (P) đi qua các điểm A (0

PT

Pham Trong Bach

8 tháng 11 2019

Viết phương trình của Parabol (P) biết rằng (P) đi qua các điểm A (0; 2), B (-2; 5), C (3; 8) A. y = 7 10 x 2 + 1 10 x − 2 B. y = 7 10 x 2 − 1 10 x + 2 C. y = 7 10 x 2 − 1 10 x − 2 D. y = 7 10 x 2 + 1 10 x + 2 ...

Đọc tiếp

#Toán lớp 10

1

CM

Cao Minh Tâm

8 tháng 11 2019

Đáp án B

Đúng(0)

QT

Quoc Tran Anh Le

Giáo viên

1 tháng 10 2023

Cho hàm số \(y = f(x) = a{x^2} + bx + c\) với đồ thị là parabol (P) có đỉnh \(I\left( {\frac{5}{2}; - \frac{1}{4}} \right)\) và đi qua điểm \(A(1;2)\)a) Biết rằng phương trình của parabol có thể viết dưới dạng \(y = a{(x - h)^2} + k\), tron đó I(h;k) là tọa độ đỉnh của parabol. Hãy xác định phương trình của parabol (P) đã cho và vẽ parabol này.b) Từ parabol (P) đã vẽ ở câu a, hãy cho biết khoảng đồng biến và khoảng nghịch...

Đọc tiếp

#Toán lớp 10

1

HQ

Hà Quang Minh

Giáo viên

1 tháng 10 2023

a) Parabol: \(y = a{(x - h)^2} + k\) với \(I(h;k) = \left( {\frac{5}{2}; - \frac{1}{4}} \right)\) là tọa độ đỉnh.

\( \Rightarrow y = a{\left( {x - \frac{5}{2}} \right)^2} - \frac{1}{4}\)

(P) đi qua \(A(1;2)\) nên \(2 = a{\left( {1 - \frac{5}{2}} \right)^2} - \frac{1}{4} \Rightarrow a = 1\)

\( \Rightarrow y = {\left( {x - \frac{5}{2}} \right)^2} - \frac{1}{4} \Leftrightarrow y = {x^2} - 5x + 6\)

Vậy parabol đó là \(y = {x^2} - 5x + 6\)

b) Vẽ parabol \(y = {x^2} - 5x + 6\)

+ Đỉnh \(I\left( {\frac{5}{2}; - \frac{1}{4}} \right)\)

+ Giao với Oy tại điểm \((0;6)\)

+ Giao với Ox tại điểm \((3;0)\) và \((2;0)\)

+ Trục đối xứng \(x = \frac{5}{2}\). Điểm đối xứng với điểm \((0;6)\) qua trục đối xứng có tọa độ \((5;6)\)

b) Hàm số đồng biến trên khoảng \(\left( { - \frac{5}{2}; + \infty } \right)\)

Hàm số nghịch biến trên khoảng \(\left( { - \infty ; - \frac{5}{2}} \right)\)

c) \(f(x) \ge 0 \Leftrightarrow {x^2} - 5x + 6 \ge 0\)

Cách 1: Quan sát đồ thị, ta thấy các điểm có\(y \ge 0\) ứng với hoành độ \(x \in ( - \infty ;2] \cup [3; + \infty )\)

Do đó tập nghiệm của BPT \(f(x) \ge 0\) là \(S = ( - \infty ;2] \cup [3; + \infty )\)

Cách 2:

\(\begin{array}{l} \Leftrightarrow {x^2} - 5x + 6 \ge 0\\ \Leftrightarrow (x - 2)(x - 3) \ge 0\end{array}\)

Do đó \(x - 2\) và \(x - 3\) cùng dấu. Mà \(x - 2 > x - 3\;\forall x \in \mathbb{R}\)

\( \Leftrightarrow \left[ \begin{array}{l}x - 3 \ge 0\\x - 2 \le 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x \ge 3\\x \le 2\end{array} \right.\)

Tập nghiệm của BPT là \(S = ( - \infty ;2] \cup [3; + \infty )\)

Đúng(0)

HA

Híp Ai Đồ

21 tháng 2 2016 - olm

a. Viết phương trình đường thẳng đi qua gốc tọa độ O và điểm M(2;4)

b. Viết phương trình parabol dạng y= a.x^2 và đi qua điểm M(2;4)

c. Vẽ parabol và đường thẳng trên trong cùng một hệ trục tọa độ và tìm tọa độ giao điểm của chúng. Help me! Thanks :)

#Toán lớp 9

0

ND

Nguyễn Duy Khánh

11 tháng 2 2021

Trong mặt phẳng Oxy, cho parabol P : y = -x 2 và đường thẳng d đi qua điểm M 0;-1 có hệ số góc k. c Viết phương trình đường thẳng d . Chứng minh rằng với mọi giá trị của ,k d luôn cắt P tại hai điểm phân biệt A,B. giúp mình nha

#Toán lớp 9

0

VN

Vương Nguyệt Nguyệt

20 tháng 12 2020

Viết phương trình parabol đi qua A (0;-1),B(1;-1),C(-1;1)

#Toán lớp 10

1

HP

Hồng Phúc

20 tháng 12 2020

\(y=ax^2+bx+c\left(a\ne0\right)\)

\(\left\{{}\begin{matrix}c=-1\\a+b+c=-1\\a-b+c=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=-1\\c=-1\end{matrix}\right.\)

\(\Rightarrow y=x^2-x-1\)

Đúng(0)

VA

Vu Anh Minh

21 tháng 3 2018 - olm

Trong mặt phẳng toạ độ Oxy,cho parabol(P):y=-x² và đường thẳng (d) đi qua điểm I(0;1) có hệ số góc k

Viết phương trình đường thẳng (d).Chứng minh rằng :Với mọi giá trị của k, đường thẳng (d) luôn cắt parabol(P) tại hai điểm phân biệt A và B

#Toán lớp 9

0

PT

Pham Trong Bach

7 tháng 1 2017

Viết phương trình parabol đi qua các điểm cực trị của đồ thị C : y = x 3 - 3 x 2 + 4 và tiếp xúc với đường thẳng y = -2x + 2 A. y = 2 x 2 - 6 x + 4 B. y = 2 x 2 + 6 x + 4 C. y = 2 x 2 - 6 x - 4 D. y = - 2 x 2 + 6 x + 4 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

7 tháng 1 2017

(C) có hai điểm cực trị là A ( 0;4 ); B ( 2;0 )

Gọi (P): a x 2 + b x + c a ≠ 0 là parabol cần tìm.

Ta có

A , B ∈ P ⇒ c = 4 4 a + 2 b + c = 0 ⇒ b = - 2 a - 2 c = 4

Khi đó: (P): y = a x 2 - 2(a + 1 )x + 4

(P) tiếp xúc với đường thẳng y = -2x + 2 khi và chỉ khi hệ sau có nghiệm:

a x 2 - 2 a + 1 x + 4 1 2 a x - 2 a + 1 = - 2 1 = - 2 x + 2 ⇒ a = 2 ⇒ b = - 6

Vậy parabol (P): y = 2 x 2 - 6 x + 4

Đáp án A

Đúng(0)

VD

Võ Đăng Khoa

29 tháng 4 2016

Cho hàm số \(y=\left(2-x\right)^2x^2\) có đồ thị (C)

a. Viết phương trình tiếp tuyến tại giao điểm (C) với Parabol \(y=x^2\)

b. Viết phương trình tiếp tuyến của (C), biết tiếp tuyến đi qua điểm A(2;0)

#Toán lớp 12

1

TM

Trần Minh Ngọc

3 tháng 5 2016

Ta có \(y=x^4-4x^3+4x^2\Rightarrow4x^3-12x^2+8x\)

a. PTHD giao điểm của (C) và Parabol \(y=x^2\) :

\(x^4-4x^3+4x^2=x^2\Leftrightarrow x^2\left(x^2-4x+3\right)=0\)

\(\Leftrightarrow x=0;x=1;x=3\)

* \(x=0\) ta có phương trình tiếp tuyến là \(y=0\)

* \(x=2\) ta có phương trình tiếp tuyến là \(y=1\)

* \(x=3\) ta có phương trình tiếp tuyến là \(y=24x-63\)

b. Gọi d là đường thẳng đi qua A, có hệ số góc k \(\Rightarrow d:y=k\left(x-2\right)\)

d là tiếp tuyến \(\Leftrightarrow\begin{cases}\left(2-x\right)^2x^2-k\left(x-2\right)\\4x\left(x-2\right)\left(x-1\right)=k\end{cases}\) có nghiệm

Thay k vào phương trình thứ nhất ta có :

\(x^4-4x^3+4x^2=\left(x-2\right)\left(4x^3-12x^2+8x\right)\)

\(\Leftrightarrow x\left(3x-4\right)\left(x-2\right)^2=0\)

\(\Leftrightarrow x=0;x=2;x=\frac{4}{3}\)

* \(x=0\Rightarrow k=0\Rightarrow\) Phương trình tiếp tuyến \(y=0\)

* \(x=2\Rightarrow k=0\Rightarrow\) Phương trình tiếp tuyến \(y=0\)

* \(x=\frac{4}{3}\Rightarrow k=-\frac{32}{27}\Rightarrow\) Phương trình tiếp tuyến \(y=-\frac{32}{27}x+\frac{64}{27}\)

Đúng(0)

PT

Pham Trong Bach

3 tháng 4 2018

Xác định parabol (P): y = ax² + bx + c biết rằng parabol (P) đi qua ba điểm A(1; 1), B(-1; -3) và O(0; 0).

A. y = x² + 2x.

B. y = -x² – 2x.

C. y = -x² + 2x.

D. y = x² – 2x.

#Toán lớp 10

1

CM

Cao Minh Tâm

3 tháng 4 2018

Vì parabol đi qua ba điểm A, B, C nên ta có hệ phương trình:

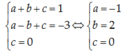
Vậy (P): y = -x² + 2x

Chọn C.

Đúng(0)

NP

Nhỏ Poki

10 tháng 5 2020 - olm

Bài 9 : Cho parabol y = ax² và điểm A(– 2 ; – 1)

a) Xác định hệ số a biết parabol đi qua điểm A.

b) Viết phương trình đường thẳng d tiếp xúc với parabol tại điểm A.

#Toán lớp 9

3

KS

Kudo Shinichi

10 tháng 5 2020

Vì P đi qua điểm A

Thay vèo ta cóa \(-1=a.4\Rightarrow a=-\frac{1}{4}\)

Ý b thiếu dữ kiện à bn ơi ?

Đúng(1)

ZH

ミ★Zero ❄ ( Hoàng Nhật )

10 tháng 5 2020

í b thiếu dữ kiện

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP