cho \(\Delta\)ABC = \(\Delta\) MNP với M = 40 độ ; 3B = 4C. tính số đo các góc của Δ ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét ΔABC vuông tại A và ΔMNP vuông tại M có
AB=MN
BC=NP
Do đo: ΔABC=ΔMNP

Khẳng định d) là khẳng định không đúng
=> ΔACB \(\backsim\) ΔMPN

a) Ta có: \(\Delta ABC \backsim \Delta MNP\) suy ra \(\frac{{AB}}{{MN}} = \frac{{BC}}{{NP}}\,\,\left( 1 \right)\) và \(\widehat B = \widehat N\)
Mà D là trung điểm BC và Q là trung điểm NP nên \(BC = 2BD\) và \(NP = 2NQ\)
Thay vào biểu thức (1) ta được \(\frac{{AB}}{{MN}} = \frac{{2BD}}{{2NQ}} \Rightarrow \frac{{AB}}{{MN}} = \frac{{BD}}{{NQ}}\)
Xét tam giác ABD và tam giác MNQ có:
\(\frac{{AB}}{{MN}} = \frac{{BD}}{{NQ}}\) và \(\widehat B = \widehat N\)
\( \Rightarrow \Delta ABD \backsim \Delta MNQ\) (c-g-c)
b) Vì \(\Delta ABD \backsim \Delta MNQ\) nên ta có \(\frac{{AB}}{{MN}} = \frac{{AD}}{{MQ}}\,\,\left( 2 \right)\) và \(\widehat {BAD} = \widehat {NMQ}\) hay \(\widehat {BAG} = \widehat {NMK}\)
Mà G và K lần lượt là trọng tâm của tam giác ABC và tam giác MNP nên \(AD = \frac{3}{2}AG\) và \(MQ = \frac{3}{2}MK\).
Thay vào (2) ta được: \(\frac{{AB}}{{MN}} = \frac{{\frac{3}{2}AG}}{{\frac{3}{2}MK}} \Rightarrow \frac{{AB}}{{MN}} = \frac{{AG}}{{MK}}\)
Xét tam giác ABG và tam giác NMK có:
\(\frac{{AB}}{{MN}} = \frac{{AG}}{{MK}}\) và \(\widehat {BAG} = \widehat {NMK}\)
\( \Rightarrow \)\(\Delta ABG \backsim \Delta MNK\) (c-g-c)

Bài 1:
ΔABC=ΔDEF
nên \(\widehat{A}=\widehat{D}=90^0;\widehat{B}=\widehat{E};\widehat{C}=\widehat{F}\)
mà \(\widehat{B}-\widehat{C}=20^0\)
nên \(\widehat{E}-\widehat{F}=20^0\)
mà \(\widehat{E}+\widehat{F}=90^0\)
nên \(\widehat{E}=\dfrac{1}{2}\left(20^0+90^0\right)=55^0\)
=>\(\widehat{F}=35^0\)

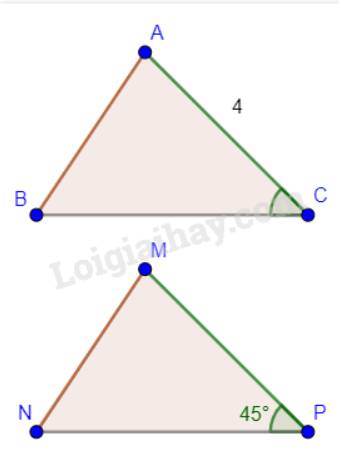
\(\Delta ABC = \Delta MNP\) nên \(AC = MP\)và \(\widehat {MPN} = \widehat {ACB}\).
Vậy \(MP = 4\)cm và \(\widehat {ACB} = 45^\circ \).

Vì \(\Delta ABC=\Delta MNP\) nên:
N = B = 60o (2 góc tương ứng)
C = P = 30o (2 góc tương ứng)
Nên A = M = 180o - (60o + 30o) = 90o
Vậy \(\Delta ABC,\Delta MNP\) là các tam giác vuông (có góc bằng 90o)
Do: \(\Delta ABC=\Delta MNP\left(gt\right)\)
\(\Rightarrow\widehat{A}=\widehat{M}=40^o\) (hai góc tương ứng)
Mà: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=180^o-40^o=140^o\)
\(\Rightarrow3\widehat{B}+3\widehat{C}=3\cdot140^o\)
Lại có: \(3\widehat{B}=4\widehat{C}\)
\(\Rightarrow4\widehat{C}+3\widehat{C}=420^o\)
\(\Rightarrow7\widehat{C}=420^o\Rightarrow\widehat{C}=60^o\)
\(\Rightarrow\widehat{\text{B}}=140^o-60^o=80^o\)
Do ∆ABC = ∆MNP (gt)
⇒ ∠A = ∠M = 40⁰
Ta có:
∠A + ∠B + ∠C = 180⁰ (tổng ba góc trong ∆ABC)
⇒ ∠B + ∠C = 180⁰ - ∠A
= 180⁰ - 40⁰
= 140⁰
⇒ 3(∠B + ∠C) = 3.140⁰
⇒ 3∠B + 3∠C = 420⁰
Mà 3∠B = 4∠C
⇒ 4∠C + 3∠C = 420⁰
⇒ 7∠C = 420⁰
⇒ ∠C = 420⁰ : 7
⇒ ∠C = 60⁰
⇒ ∠B = 140⁰ - ∠C
= 140⁰ - 60⁰
= 80⁰
Vậy số đo các góc của ∆ABC là:
∠A = 40⁰; ∠B = 80⁰; ∠C = 60⁰