Số các giá trị nguyên của tham M ∈ - 2019 ; 2019 để hàm số y = m + 1 x 2 - 2 m x + 6 m x - 1 đồng biến trên khoảng 4 ; + ∞ ?
A. 2034
B. 2018
C. 2025
D. 2021
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
Đồ thị hàm số y=f(x-2019) được tạo thành bằng cách tịnh tiến đồ thị hàm số y=f(x) theo chiều song song với trục Ox sang bên phải 2019 đơn vị.
Đồ thị hàm số y=f(x-2019)+m-2 được tạo thành bằng cách tịnh tiến đồ thị hàm số y=f(x-2019) theo chiều song song với trục Oy lên trên m-2 đơn vị.
Đồ thị hàm số y=|f(x-2019)+m-2| được tạo thành bằng cách giữ nguyên phần đồ thị y=f(x-2019)+m-2 phía trên trục Ox, lấy đối xứng toàn bộ phần đồ thị phía dưới trục Ox qua trục Ox và xóa đi phần đồ thị phía dưới trục Ox.
Do đó để đồ thị hàm số y=|f(x-2019)+m-2| có 5 điểm cực trị thì đồ thị hàm số y=f(x-2019)+m-2 có


Để phương trình có nghiệm thì \(\left(\sqrt{2019}\right)^2+\left(-1\right)^2>=4m^2\)
=>4m^2<=2020
=>m^2<=505
mà m nguyên
nên \(m^2\in\left\{0;1;...;22^2\right\}\)
=>\(m\in\left\{-22;-21;...;21;22\right\}\)
=>Tổng các phần tử là 0
=>Chọn D

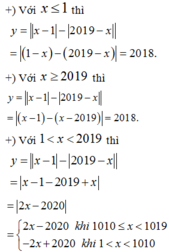
Do đó
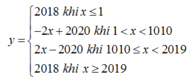
Vẽ dáng đồ thị hàm số ta được:
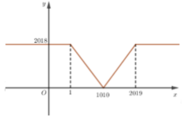
Từ hình vẽ ta thấy phương trình đã cho có nghiệm nếu đường thẳng y = 2020 - m cắt đồ thị hàm số trên tại ít nhất một điểm hay

giá trị của m thỏa mãn bài toán.
Chọn D.

Chọn A.
TXĐ: D = R
Ta có: y ' = 3 x 2 - 6 x + 3 m
Để hàm số đã cho nghịch biến trên 1 ; 2
thì y ' ≤ 0 , ∀ x ∈ 1 ; 2 và bằng 0 tại hữu hạn điểm
![]()
![]()
![]()
![]()
Hàm số y = x - 1 2 đồng biến trên 1 ; + ∞ nên cũng đồng biến trên 1 ; 2
![]()
![]()
Lại có m ∈ - 10 ; 10 và m ∈ Z nên m ∈ - 10 ; - 9 ; . . ; 0
Vậy có 11 giá trị của m
ĐK: x#1
Ta có
Để hàm số đồng biến trên 4 ; + ∞ thì y ' ≥ 0 ; ∀ x > 4
+ Với m+1=0 ⇔ m=-1 ⇒ 0>-4 (luôn đúng) nên nhận m=-1.(1)
+ Với m+1>0
Xét hàm số g ( x ) = x 2 - 2 x có g ' ( x ) = 2 x - 2 = 0 ⇔ x = 1 ∉ 4 ; + ∞ , ta có BBT trên 4 ; + ∞ là
Từ BBT suy ra
+ Với m+1<0 ⇔ m < - 1
Từ BBT của g(x) suy ra không có m thỏa mãn.
Từ (1) và (2) suy ra m ≥ - 1 mà m ∈ - 2019 ; 2019 và m nguyên nên m ∈ - 1 ; 0 ; . . ; 2019 ⇒ có 2021 số thỏa mãn.
Chọn đáp án D.