Viết phương trình mặt phẳng (P) đi qua điểm A (0; -1; 2), song song với trục Ox và vuông góc với mặt phẳng (Q) : x + 2y - 2z +1 = 0.
A. (P) : 2y + 2z - 1 = 0
B. (P) : y + z - 1 = 0
C. (P) : y - z + 3 = 0
D. (P) : 2x + z - 2 = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn A
Mặt phẳng (Q) qua điểm O và nhận vectơ pháp tuyến là tích có hướng của vecto OA và vecto pháp tuyến của mặt phẳng (P)

Cách 1:
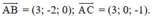
Mặt phẳng (R) đi qua ba điểm A, B, C nhận 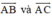 là hai vec tơ chỉ phương
là hai vec tơ chỉ phương
⇒ Nhận 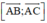 = ((-2).(-1) – 0; 0.3 – 3.(-1); 3.0 – 3.(-2)) = (2; 3; 6) là vec tơ pháp tuyến.
= ((-2).(-1) – 0; 0.3 – 3.(-1); 3.0 – 3.(-2)) = (2; 3; 6) là vec tơ pháp tuyến.
(R) đi qua A(-3; 0; 0) nên có phương trình:
2(x + 3) + 3y + 6z = 0
⇔ 2x + 3y + 6z + 6 = 0.
Cách 2 :
(R) đi qua A(-3 ; 0 ; 0) ; B(0 ; -2 ; 0) ; C(0 ; 0 ; -1) nên có phương trình đoạn chắn là :
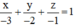
⇔ 2x + 3y + 6z + 6 = 0.

Đáp án D
Ta có: A B → = ( - 3 ; - 2 ; 2 ) ; n ( P ) → = ( 1 ; - 3 ; 2 )
Khi đó: A B → ; n ( P ) → = 0 ; 8 ; 12 ⇒ n ( Q ) → = ( 0 ; 2 ; 3 )
Suy ra (Q): 2y + 3z – 11 = 0