Chứng minh từ A( 1; -1) kẻ được 2 tiếp tuyến vuông góc tới đồ thị hàm số \(y=x+\dfrac{1}{x+1}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 6 2023
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
b: Xét ΔAEM vuông tại E và ΔAFM Vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF
=>ΔAFE cân tại A
c: AE=AF
ME=MF
=>AM là trung trực của FE
d: Xét ΔEFI có
EM là trung tuyến
EM=FI/2
=>ΔEFI vuông tại E
=>EF vuông góc FI
=>FI//AM
21 tháng 12 2021
a: Xét tứ giác OMAN có
\(\widehat{OMA}+\widehat{ONA}=180^0\)
Do đó: OMAN là tứ giác nội tiếp
9 tháng 12 2016
a, xét tam giác AMB và tam giác AMC có :
AB=AC (gt)
MB=MC (gt)
AM là cạnh chung
suy ra: tam giác AMB = tam giác AMC (c.c.c)
b,Vì tam giác AMB = tam giác AMC ( câu a)
suy ra : góc B =góc C ( 2 góc tương ứng )
xét tam giác MBE và tam giác MCF có:
M1=M2 ( đối đỉnh )
B =C
MB=MC ( gt)
suy ra :tam giác MBE = tam giác MCF (g.c.g)
vì tam giác MBE = tam giác MCF (chứng minh trên)
ME=MF (2 cạch tương ứng )
xét tam giác AEM và tam giác AFM có :
E1=F1
AM là cạnh chung
ME=MF
suy ra : tam giác AEM = tam giác AFM (c.g.c)
vì tam giác AEM = tam giác AFM ( chứng minh trên)
suy ra :AE=AF
c, gọi điểm cắt nhau của EF và AM
Vì tam giác AMB = tam giác AMC (câu b)
suy ra : góc A1 = góc A2 ( 2 góc tương ứng ); góc M1 = góc M2 ( 2 góc tương ứng)
xét tam giác AEH và tam giác AFH có :
A1=A2
AE=AF
AH là điểm chung
suy ra : tam giác AEH = tam giác AFH (c.g.c)
suy ra góc H1= góc H2 ( 2 góc tương ứng)
mà H1+H2=180 (2 góc kề bù)
suy ra : H1=H2=90
suy ra AM vuông góc với EF
mà M1+M2=180
suy ra M1=M2=90
suy ra AM vuông góc với BC
mà AM vuông góc với EF
suy ra EF song song với BC ( 2 đường thẳng phân biệt cùng vuông góc với đường thẳng thứ 3 thì chúng song song với nhau )
d, Ta có : AMB = NMC ( đối đỉnh )
+) AMB+AMC= 180 ( 2 góc kề bù )
mà AMC=NMC
suy ra AMB+NMC =180 (3)
mà AMB+NMC = AMN (4)
Từ (3),(4) suy ra : 3 điểm A,M,N thẳng hàng
9 tháng 12 2016
1, xét tam giác AMB và tam giác AMC có:
AB=AC (gt)
MB=MC (gt)
12 tháng 5 2021
a) Xét ΔABM và ΔACM có:
AB=AC ( ΔABC cân tại A)
Cạnh AM chung
MB=MC (gt)
⇒ ΔABM=ΔACM (c.c.c)
Vậy ΔABM=ΔACM
b) Vì ΔABM=ΔACM (cmt)
⇒ ∠AMB=∠AMC (2 góc tương ứng)
Ta có:∠AMB+∠AMC=180 ( 2 góc kề bù)
⇒ AMB=AMC=1800/2=900
⇒ AM⊥BC
Vậy AM⊥BC
c) Vì MK⊥AC (gt)
⇒ ∠MKA=∠MKC=900
Vì MH⊥AB (gt)
⇒ ∠MHA=∠MHB=900
Xét ΔHBM và ΔKCM có:
∠MHB∠=MKC=900
MB=MC (gt)
∠HMB∠=KMC (đối đỉnh)
⇒ ΔHBM = ΔKCM (cạnh huyền - góc nhọn)
⇒ BH=CK (2 cạnh tương ứng)
Vậy BH=CK
Mik mỏi tay lám rùi bạn tự làm phần sau nhé
12 tháng 5 2021
xét ΔABM và ΔACM có:
AB=AC(ΔABC cân tại A)
\(\widehat{ABM}=\widehat{ACM}\)(ΔABC cân tại A)
BM=CM(M là trung điểm của BC)
⇒ΔABM=ΔACM(c-g-c)
⇒\(\widehat{AMB}=\widehat{AMC}\)(2 góc tương ứng)(1)
Mà \(\widehat{AMB}+\widehat{AMC}=180^o\)(2 góc kề bù)(2)
từ (1)và(2)⇒\(\widehat{ABM}=\widehat{ACM}=\dfrac{180^o}{2}=90^o\)
hay AM⊥BC(đ.p.ch/m)
xét 2 tam giác vuông HBM và KCM có
MC=MB(M là trung điểm của BC)
\(\widehat{HBM}=\widehat{KCM}\)(ΔABC cân tại A)
⇒ΔHBM=ΔKCM(c.huyền.g.nhọn)
⇒BH=CK(2 cạnh tương ứng)
vì BP⊥AC và MK⊥AC⇒BP//MK
vì ΔHBM=ΔKCM nên
⇒\(\widehat{HMB}=\widehat{KMC}\)(2 góc tương ứng)
Mà \(\widehat{KMC}=\widehat{PBM}\)(2 góc đồng vị)
⇒ΔIBM là tam giác cân(đ.p.ch/m)
vì BP⊥AC và MK⊥AC⇒BP//MK(đ.p.ch/m)
CM
16 tháng 5 2018
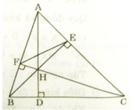
a) Xét ΔAEB và ΔAFC có:
∠AEB = ∠AFC = 90o (gt)
∠A chung
Vậy ΔAEB ∼ ΔAFC (g.g)
b) Xét ΔAEF và ΔABC có
∠A chung
AF.AB = AE.AC (Cmt)
⇒ ΔAEF ∼ ΔABC (c.g.c)
⇒ ∠AEF = ∠ABC
c) ΔAEF ∼ ΔABC (cmt)
. Đường thẳng ED cắt BA tại F.
?
30 tháng 7 2021
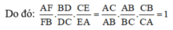
a) Xét ΔBDA vuông tại A và ΔBDE vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác)
Do đó: ΔBDA=ΔBDE(cạnh huyền-góc nhọn)
b) Ta có: ΔBDA=ΔBDE(cmt)
nên BA=BE(hai cạnh tương ứng) và DA=DE(Hai cạnh tương ứng)
Ta có: BA=BE(cmt)
nên B nằm trên đường trung trực của AE(1)
Ta có: DA=DE(cmt)
nên D nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE
\(y'=1-\dfrac{1}{\left(x+1\right)^2}=\dfrac{x^2+2x}{\left(x+1\right)^2}\)
Gọi đường thẳng d qua A có dạng: \(y=k\left(x-1\right)-1\)
d là tiếp tuyến của (C) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{x^2+x+1}{x+1}=k\left(x-1\right)-1\\\dfrac{x^2+2x}{\left(x+1\right)^2}=k\end{matrix}\right.\) có nghiệm
\(\Rightarrow\dfrac{x^2+x+1}{x+1}=\dfrac{\left(x-1\right)\left(x^2+2x\right)}{\left(x+1\right)^2}-1\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+x+1\right)=\left(x-1\right)\left(x^2+2x\right)-\left(x+1\right)^2\)
\(\Leftrightarrow x^2+3x+1=0\) \(\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{-3+\sqrt{5}}{2}\\x_2=\dfrac{-3-\sqrt{5}}{2}\end{matrix}\right.\)
\(\left(1-\dfrac{1}{\left(x_1+1\right)^2}\right)\left(1-\dfrac{1}{\left(x_2+1\right)^2}\right)=-1\Rightarrow\) hai tiếp tuyến kẻ từ A vuông góc nhau
Không thích tính toán thì từ \(x^2+3x+1=0\Rightarrow x^2+2x=-x-1\) thế vào \(y'=\dfrac{x^2+2x}{\left(x+1\right)^2}=\dfrac{-1}{x+1}\)
Do đó \(k_1k_2=-\dfrac{1}{x_1+1}.\left(-\dfrac{1}{x_2+1}\right)=\dfrac{1}{x_1x_2+x_1+x_2+1}=\dfrac{1}{1-3+1}=-1\)