Cho hai điểm A,B thuộc đồ thị hàm số y=sinx trên đoạn 0 ; π , các điểm C,D thuộc trục Ox sao cho tứ giác ABCD là hình chữ nhật và C D = 2 π 3 .
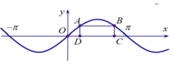
Độ dài đoạn thẳng BC bằng
A. 2 2 .
B. 1 2 .
C.1
D. 3 2 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp giải:
Dựa vào đồ thị hàm số xác định hoành độ điểm D suy ra tung độ điểm A chính là độ dài BC
Lời giải: Gọi ![]() với
với ![]()
Gọi ![]() thuộc đồ thị
thuộc đồ thị ![]()
Vì ABCDlà hình chữ nhật ![]()
Khi đó BC = m. Mà ![]()
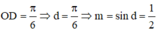

Đáp án là D.
Xét phương trình hoành độ giao điểm sin x = cos x ⇔ sin x − cos x = 0 ∗
Số giao điểm của hai đồ thị hàm số chính là số nghiệm của phương trình (*) trên − 2 π ; 5 π 2 .
Khi đó ta có sin x − cos x = 0 ⇔ 2 sin x − π 4 = 0 ⇔ x = π 4 + k π , k ∈ ℤ .
Mà x ∈ − 2 π ; 5 π 2 nên ta có − 2 π ≤ π 4 + k π ≤ 5 π 2 − 2 π ≤ π 4 + k π ≤ 5 π 2 .
Hay ta có k ∈ − 2 ; − 1 ; 0 ; 1 ; 2 .

Chọn C
Phương trình hoành độ giao điểm của hai đồ thị hàm số là: sinx = cosx

Vậy đồ thị hai hàm số đã cho cắt nhau tại 5 điểm trên đoạn - 2 π ; 5 π 2

a)
f(0) = 2 . 0 - 2 = -2
f(1) = 2.1 - 2 = 0
f(-1)= 2.(-1) - 2 = -4
b) Thay tọa độ A,B vào phương trình đồ thị hàm số ta có :
A : -2 = 2. 0 - 2 đúng=> A \(\in\)u= 2x -2
B: 1 = 2 . (-1) - 2 sai => B \(\in\)y =2x - 2
c) \(C\in y=2x-2\Rightarrow2=2m-2\Leftrightarrow m=2\)

Đáp án A
Vì điểm A(1; 2) thuộc đồ thị hàm số y = a x 2 (a ≠ 0) nên:
2 = a. 1 2 ⇒ a = 2
Vây hàm số đã cho là y = 2 x 2 .
Trong các điểm đã cho chỉ có điểm M (2; 8) thuộc đồ thị hàm số.