Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Phương trình hoàn độ giao điểm của hai đồ thì hàm số là \(\sin x = \cos x\)
\( \Leftrightarrow \tan x = 1 \Leftrightarrow x = \frac{\pi }{4} + k\pi \;\left( {k \in \mathbb{Z}} \right)\)
Do \(x \in \left[ { - 2\pi ;\frac{{5\pi }}{2}} \right]\; \Leftrightarrow - 2\pi \le \frac{\pi }{4} + k\pi \le \frac{{5\pi }}{2}\;\; \Leftrightarrow \; - \frac{9}{4} \le k \le \frac{9}{4}\;\;\;\)
Mà \(k\; \in \mathbb{Z}\;\; \Leftrightarrow k\; \in \left\{ { - 2;\; - 1;0;1;2} \right\}\)
Vậy ta chọn đáp án A

a) Vẽ đồ thị:
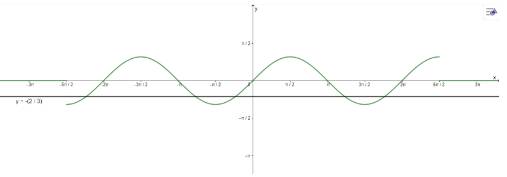
\(3\sin x + 2 = 0\) trên đoạn \(\left( { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)\) có 5 nghiệm
b) Vẽ đồ thị:

\(\cos x = 0\) trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\) có 6 nghiệm

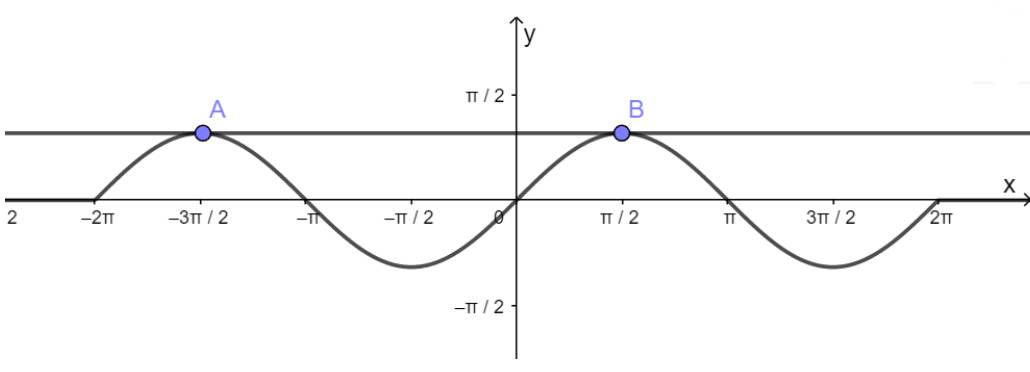
a) Hàm số y = sinx nhận giá trị bằng 1
- Vẽ hàm số y = sinx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = 1
- Lấy giao điểm của hai hàm số y = sinx và y = 1 là A, B,...
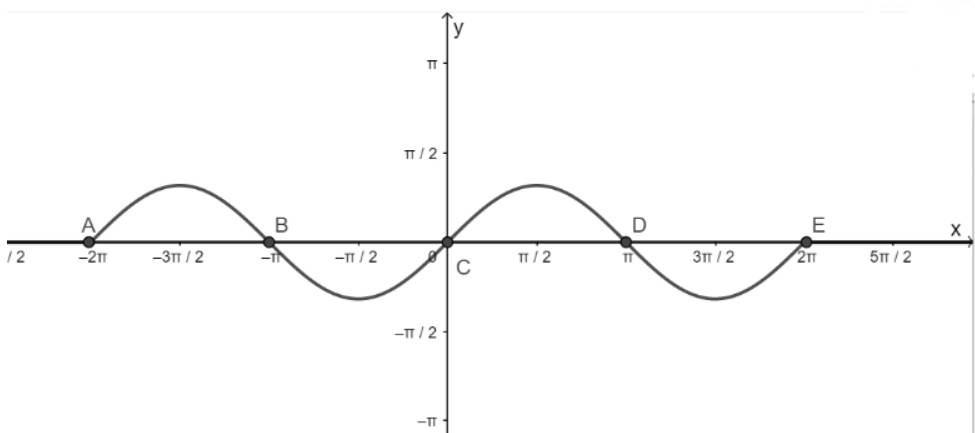
b) Hàm số y = sinx nhận giá trị bằng 0
- Vẽ hàm số y = sinx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = sinx và y = 0 là A, B, C, D, E,...
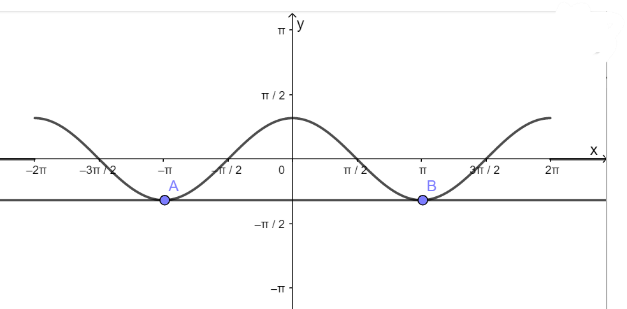
c) Hàm số y = cosx nhận giá trị bằng – 1
- Vẽ hàm số y = cosx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = - 1
- Lấy giao điểm của hai hàm số y = cosx và y = - 1 là A, B,...
d) Hàm số y = cosx nhận giá trị bằng 0
- Vẽ hàm số y = cosx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = 0
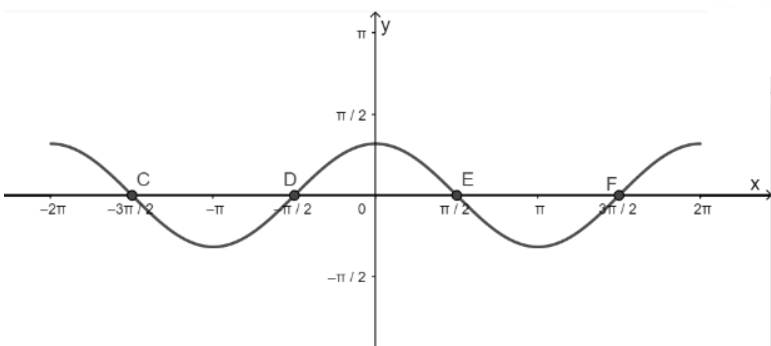
- Lấy giao điểm của hai hàm số y = cosx và y = 0 là C, D, E, F,...

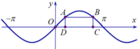
y = \(\dfrac{sin^2x}{cosx\left(sinx-cosx\right)}+\dfrac{1}{4}\)
y = \(\dfrac{sin^2x}{sinx.cosx-cos^2x}+\dfrac{1}{4}=\dfrac{\dfrac{sin^2x}{cos^2x}}{\dfrac{sinx.cosx}{cos^2x}-1}+\dfrac{1}{4}\)
y = \(\dfrac{tan^2x}{tanx-1}+\dfrac{1}{4}\)
y = \(\dfrac{4tan^2x+tanx-1}{4tanx-4}\). Đặt t = tanx. Do x ∈ \(\left(\dfrac{\pi}{4};\dfrac{\pi}{2}\right)\) nên t ∈ (1 ; +\(\infty\))\
Ta đươc hàm số f(t) = \(\dfrac{4t^2+t-1}{4t-4}\)
⇒ ymin = \(\dfrac{17}{4}\) khi t = 2. hay x = arctan(2) + kπ
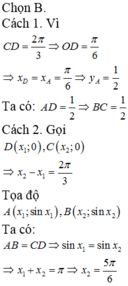
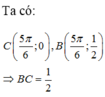

Chọn C
Phương trình hoành độ giao điểm của hai đồ thị hàm số là: sinx = cosx
Vậy đồ thị hai hàm số đã cho cắt nhau tại 5 điểm trên đoạn - 2 π ; 5 π 2