Cho hình vuông ABCD có cạnh 10cm. Lấy điểm M trên cạnh AB; điểm N trên cạnh BC; điểm P trên cạnh CD sao cho \(AM=\frac{1}{4}AB\) và BN = NC. Nối M với N; N với P; P với M. Tính diện tích lớn nhất và nhỏ nhất có thể của tam giác MNP.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Yêu cầu đề bài là gì vậy bạn? Nếu là tìm diện tích tam giác $AMD$ thì:
$S_{AMD}=\frac{1}{3}S_{ABCD}=\frac{1}{3}.15.15=75$ (cm2)

Diện tích hình thang abcd là
(45+36)×40:2=1620(cm2)
Chiều cao của hình tam giác ABC là
40-10=30(cm)
Diện tình hình tam giác ABN là
36×30:2=540(cm2)
Diện tích hình tam giác ncd là
45×10:2=225(cm2)
Diện tích hình tam giác and là
1620-(540+225)=855(cm)
Đáy lớn của hình thang abnm là
855×2:40=42,75(cm)
Diện tích hình thang abnm là
(36+42,75)×30:2=1181,25(cm2)
ĐS:1181,25cm2
Diện tích hình thang abcd là
(45+36)×40:2=1620(cm2)
Chiều cao của hình tam giác ABC là
40-10=30(cm)
Diện tình hình tam giác ABN là
36×30:2=540(cm2)
Diện tích hình tam giác ncd là
45×10:2=225(cm2)
Diện tích hình tam giác and là
1620-(540+225)=855(cm)
Đáy lớn của hình thang abnm là
855×2:40=42,75(cm)
Diện tích hình thang abnm là
(36+42,75)×30:2=1181,25(cm2)
ĐS:1181,25cm2

: Ký hiệu (a) là số đo góc a, đặt (CDK)=x
trên tia đối tia AB lấy điểm F sao cho AF = KC
như vậy tam giác ADF bằng tam giác CDK nên góc (ADF)=(CDK)=(KDE)=x
góc (FED)=(EDC)=2x (so le trong)
(FDE)=x+(90-2x)= 90-x
(EFD) = 180 - (FED) - (FDE) = 180 -( 2x) -(90-x) = 90-x = (FDE) vậy tam giác FED cân tại E hay DE =FE = FA +AE =KC + AE dpcm

a)nửa chu vi HCN ABCD là : 100 : 2 = 50 ( cm )
nửa chu vi HCN BMNC là : 60 : 2 = 30 ( cm )
cạnh hình vuông ANND là : 50 - 30 = 20 ( cm ) _vẽ hình rồi hiểu
chiều dài HCN ABCD là : 50 - 20 = 30 ( cm )
b) diện tích DMC là :
30 x 20 : 2 = 300 ( cm2 )
ĐS:...
_HT_
#ThaoNguyen#
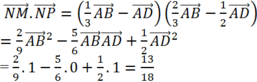
\(S_{MNP}=S_{ABCD}-\left(S_{MNB}+S_{AMPD}+S_{CNP}\right)\) (*)
\(S_{AMPD}=\frac{\left(AM+DP\right)xAD}{2}=\frac{\left(AM+DP\right)x10}{2}=5xAM+5xDP\)
\(S_{CNP}=\frac{CPxCN}{2}=\frac{5xCP}{2}\)
\(S_{AMPD}+S_{CNP}=5xAM+5xDP+\frac{5xCP}{2}=\frac{10xAM+10xDP+5xCP}{2}=\)
\(=\frac{10xAM+5x\left(DP+CP\right)+5xDP}{2}=\frac{10xAM+5xCD+5xDP}{2}\)(**)
Từ (*) ta thấy \(S_{MNP}\) phụ thuộc vào \(S_{AMPD}+S_{CNP}\) (Do \(S_{ABCD};S_{MNB}\) không thay đổi)
\(\Rightarrow S_{MNP}\) nhỏ nhất khi (**) lớn nhât và \(S_{MNP}\) lớn nhất khi (**) nhỏ nhất
(**) lớn nhất khi DP lớn nhất, DP lớn nhất khi P trùng với C
(**) nhỏ nhất khi DP nhỏ nhất, DP nhỏ nhất khi P trùng với D
Đến đây bài toán đã tường minh bạn tự làm nốt nhé