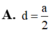
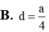
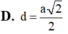
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Diện tích hình thang ABCD là:
S A B C D = A B . A D + B C 2 = 5
Vậy thể tích khối chóp S.ABCD là:
V = 1 3 . S A . S A B C D = 1 3 . S A . S A B C D = 1 3 .2.5 = 10 3 (đvtt)
Đáp án D
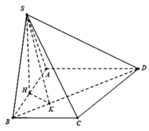
Dựng HK ⊥ BD, do SH ⊥ BD nên ta có:
(SKH) ⊥ BD => Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là góc SKH = 600
Lại có: 
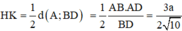
Do đó 
Vậy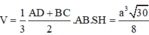 
Chọn D
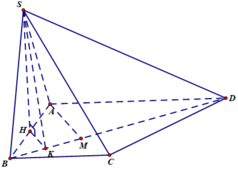
Ta có 
Gọi H là trung điểm AB thì 
,
kẻ 
, ta có 
là góc giữa (SBD) và (ABCD), do đó 
= 600
Gọi AM là đường cao của tam giác vuông ABD. Khi đó, ta có:
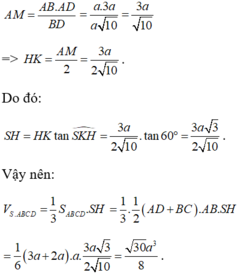
Đáp án B
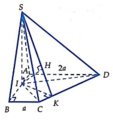
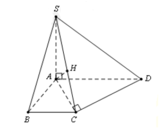
S I C D = S A B C D − S A I D − S B I C = 3 a 2 − a 2 − a 2 2 = 3 a 2 2 ; C D = 2 a 2 + a 2 = a 5
Gọi K, H lần lượt là hình chiếu của I lên CD và SK
⇒ I H ⊥ S C D ⇒ I H = d I ; S C D = 3 a 2 4
S Δ I C D = 1 2 I K . C D ⇒ I K = 2 S I C D C D = 3 a 2 a 5 = 3 a 5
1 I H 2 = 1 I K 2 + 1 I S 2 ⇒ 1 I S 2 = 8 9 a 2 − 5 9 a 2 = 1 3 a 2 ⇒ I S = a 3
⇒ V S . A B C D = 1 3 .3 a 2 . a 3 = a 3 3
Ta có tam giác ACD vuông cân tại C và CA = CD = 2a
⇒ S A A C D = 4 a 2 . Gọi H là trung điểm của AB
Vì tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy
⇒
S
H
⊥
A
B
C
D
;
S
H
=
a
3
.
V
a
y
S
S
A
C
D
=
4
a
3
3
3
Đáp án cần chọn là A
Đáp án A
Ta có tam giác ACD vuông cân tại C và C A = C D = 2 a 2
⇒ S ∆ A C D = 4 a 2 . Gọi H là trung điểm của AB
Vì tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy
⇒ S H ⊥ ( A B C D ) ; S H = a 3 .
Vậy S S . A C D = 4 a 3 3 3 .
