Cho khối chóp S.ABC có đáy ABC là tam giác cân tại A, AB = a, B A C ^ = 120 0 ; S B A ^ = S C A ^ = 90 0 Biết góc giữa SB và đáy bằng 60 0 . Tính thể tích V của khối chóp S.ABC
A. V = a 3 4
B. V = 3 a 3 3 4
C. V = a 3 3 4
D. V = 3 a 3 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
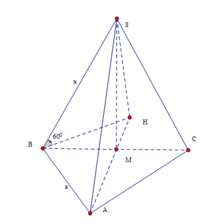
Gọi M là trung điểm BC khi đó B C ⊥ ( S A M ) do AB=AC và SB=SC
Trong (SAM) kẻ S H ⊥ A M ta có S H ⊥ A B C góc S B H = 60 ° , đặt SB=SC=x ta có:
A M = A B . sin 30 ° = 1 2 a , B M = A B . cos 60 ° = a 3 2 ⇒ B C = a 3 , d t A B C = 1 2 A M . B C = 1 2 a 2 a 3 = a 2 3 4 , S H = S B . sin 60 ° = x 3 2 , S A = S B 2 + A B 2 = x 2 + a 2 ,
S M = S B 2 - B M 2 = x 2 - 3 a 2 4 , A H = S A 2 - S H 2 = x 2 + a 2 - 3 x 2 4 = 1 2 x 2 + 4 a 2 , M H = S M 2 - S H 2 = x 2 - 3 a 2 4 - 3 x 2 4 = 1 2 x 2 - 3 a 2
Ta có : A H - M H = A M ⇒ 1 2 x 2 + 4 a 2 - 1 2 x 2 - 3 a 2 = 1 2 a ⇔ x 2 + 4 a 2 = x 2 - 3 a 2 + a
⇔ 3 a = x 2 - 3 a 2 ⇔ x 2 = 12 a 2 ⇒ x = 2 a 3 ⇒ S H = 3 a
Như vậy V S A B C = 1 3 S H . d t A B C = 1 3 3 a . a 2 3 4 = a 3 3 4

Đáp án A
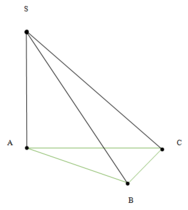
Dễ thấy ( S C , ( A B C ) ) ^ = SAC (vì SA ⊥ (ABC))
ð SA = AC.tan60° = a 3
Ta có:
V S A B C = 1 3 . S A B C . a 3 = 1 3 . 1 2 . a . a . a 3 = a 3 3 6

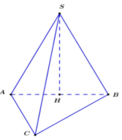
Gọi H là trung điểm của AB.
∆ S A B đều và nằm trong mặt phẳng vuông góc với
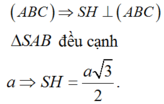
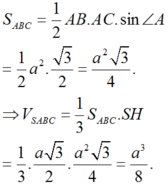
Chọn D.

Đáp án C
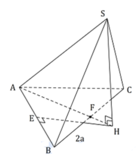
Gọi H là tâm đường tròn ngoại tiếp tam giác ABC bằng cách dựng như hình vẽ.


Đáp án C
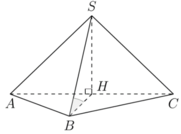
Gọi H là trung điểm AC. Ta có tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với (ABC)
suy ra S H ⊥ A B C
Ta có
S B , A B C = S B H ^ = 45 o ⇒ S H = B H = 1 2 A C = a 2 2 V S . A B C = 1 3 . a 2 2 . 1 2 a 2 = a 3 2 12