Tính hiệu P(x) – Q(x) bằng hai cách, trong đó:
\(\begin{array}{l}P(x) = 6{x^3} + 8{x^2} + 5x - 2;\\Q(x) = - 9{x^3} + 6{x^2} + 3 + 2x.\end{array}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

P(x)-Q(x)
=6x^3+8x^2+5x-2+9x^3-6x^2-2x-3
=15x^3+2x^2+2x-5
\(P\left(x\right)-Q\left(x\right)=\left(6x^3+8x^2+5x-2\right)-\left(-9x^3+6x^2+3+2x\right)\)
\(=6x^3+8x^2+5x-2+9x^3-6x^2-3-2x\)
\(=6x^3+9x^3+8x^2-6x^2+5x-2x-2-3\)
\(=15x^3+2x^2+3x-5\)

a)
\(\begin{array}{l}P(x) = 5{x^3} + 2{x^4} - {x^2} + 3{x^2} - {x^3} - 2{x^4} - 4{x^3}\\ = \left( {2{x^4} - 2{x^4}} \right) + \left( {5{x^3} - {x^3} - 4{x^3}} \right) + \left( { - {x^2} + 3{x^2}} \right)\\ = 0 + 0 + 2{x^2}\\ = 2{x^2}\\Q(x) = 3x - 4{x^3} + 8{x^2} - 5x + 4{x^3} + 5\\ = \left( { - 4{x^3} + 4{x^3}} \right) + 8{x^2} + \left( {3x - 5x} \right) + 5\\ = 0 + 8{x^2} + ( - 2x) + 5\\ = 8{x^2} - 2x + 5\end{array}\)
b) P(1) = 2.12 = 2
P(0) = 2. 02 = 0
Q(-1) = 8.(-1)2 – 2.(-1) +5 = 8 +2 +5 =15
Q(0) = 8.02 – 2.0 + 5 = 5

a) Chỗ sai trong phương trình là: \(5 - x + 8 = 3x + 3x - 27\) (dòng thứ 2) vì khi phá ngoặc đã không đổi dấu của số 8.
Sửa lại:
\(\begin{array}{l}5 - \left( {x + 8} \right) = 3x + 3\left( {x - 9} \right)\\\,\,\,\,5 - x - 8 = 3x + 3x - 27\\\,\,\,\,\,\,\, - 3 - x = 6x - 27\\\,\,\,\, - x - 6x = - 27 + 3\\\,\,\,\,\,\,\,\,\,\,\,\, - 7x = - 24\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \left( { - 24} \right):\left( { - 7} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \frac{{24}}{7}\end{array}\)
Vậy phương trình có nghiệm \(x = \frac{{24}}{7}.\)
b) Chỗ sai trong phương trình là: \(4x + 5x = 9 - 18\) (dòng thứ 3) vì khi chuyển \( - 18\) từ vế trái sang vế phải đã không đổi dấu thành \( + 18\).
Sửa lại:
\(\begin{array}{l}3x - 18 + x = 12 - \left( {5x + 3} \right)\\\,\,\,\,\,\,\,4x - 18 = 12 - 5x - 3\\\,\,\,\,\,\,\,4x + 5x = 9 + 18\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,9x = 27\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 27:9\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 3.\end{array}\)
Vậy phương trình có nghiệm \(x = 3.\)

Theo cột dọc:
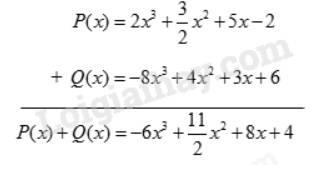
Theo hàng ngang:
\(\begin{array}{l}P(x) + Q(x) = 2{x^3} + \dfrac{3}{2}{x^2} + 5x - 2 + ( - 8){x^3} + 4{x^2} + 3x + 6\\ = (2 - 8){x^3} + (\dfrac{3}{2} + 4){x^2} + (5 + 3)x + ( - 2 + 6)\\ = - 6{x^3} + \dfrac{{11}}{2}{x^2} + 8x + 4\end{array}\)

Ta có: \(\begin{array}{l}2{\rm{x}} + 5 = 16\\2{\rm{x}} = 16 - 5\\2{\rm{x}} = 11\\x = \frac{{11}}{2}\end{array}\)
Như vậy, bạn Vuông giải đúng, bạn Tròn giải sai

\(\begin{array}{l}a)\frac{{4{\rm{x}} - 6}}{{5{{\rm{x}}^2} - x}}.\frac{{25{{\rm{x}}^2} - 10{\rm{x}} + 1}}{{27 + 8{{\rm{x}}^3}}}\\ = \frac{{ - 2\left( {3 - 2{\rm{x}}} \right)}}{{x\left( {5{\rm{x}} - 1} \right)}}.\frac{{{{\left( {5{\rm{x}} - 1} \right)}^2}}}{{\left( {3 - 2{\rm{x}}} \right)\left( {9 + 6{\rm{x}} + 4{{\rm{x}}^2}} \right)}}\\ = \frac{{ - 2\left( {5{\rm{x}} - 1} \right)}}{{x\left( {9 + 6{\rm{x}} + 4{{\rm{x}}^2}} \right)}}\\b)\frac{{2{\rm{x}} + 10}}{{{{\left( {x - 3} \right)}^2}}}:\frac{{{{\left( {x + 5} \right)}^3}}}{{{x^2} - 9}}\\ = \frac{{2{\rm{x}} + 10}}{{{{\left( {x - 3} \right)}^2}}}.\frac{{{x^2} - 9}}{{{{\left( {x + 5} \right)}^2}}}\\ = \frac{{2\left( {x + 5} \right)\left( {x - 3} \right)\left( {x + 3} \right)}}{{{{\left( {x - 3} \right)}^2}{{\left( {x + 5} \right)}^3}}}\\ = \frac{{2\left( {x + 3} \right)}}{{\left( {x - 3} \right){{\left( {x + 5} \right)}^2}}}\end{array}\)

Ta có: \(\overrightarrow {{u_1}} = \left( {1; - 2} \right) \Rightarrow \overrightarrow {{n_1}} = \left( {2;1} \right)\) và \(\overrightarrow {{u_2}} = \left( {1;3} \right) \Rightarrow \overrightarrow {{n_2}} = \left( {3; - 1} \right)\).
Ta có \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {2.3 + 1.( - 1)} \right|}}{{\sqrt {{2^2} + {1^2}} .\sqrt {{3^2} + {{( - 1)}^2}} }} = \frac{{\sqrt 2 }}{2} \\ \Rightarrow \left( {{\Delta _1},{\Delta _2}} \right) = {45^o}\)

1. \(2x^2-3x-5=0\)
\(\Leftrightarrow\left(2x-5\right)\left(x+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x-5=0\\x+1=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=2,5\\x=-1\end{cases}}\)
Vậy tập ngiệm của phương trình là \(S=\left\{2,5;-1\right\}\)
2x2-3x-5=0
2x2+2x-5x-5=0
2x(x+1)+5(x+1)=0
(x+1)(2x+5)=0
TH1 x+1=0 <=>x=-1
TH2 2x+5=0<=>2x=-5<=>x=-5/2
2. ta có:
2(x-2y)-(2x+y)=-1.2-8
2x-4y-2x-y=-2-8
-5y=-10
y=2
thay vào
x-2y=-1 ( với y=2)
<=> x-2.2=-1
x-4=-1
x=3
Theo cột dọc:
Theo hàng ngang:
\(\begin{array}{l}P(x) - Q(x) = 6{x^3} + 8{x^2} + 5x - 2 - ( - 9{x^3} + 6{x^2} + 2x + 3)\\ = 6{x^3} + 8{x^2} + 5x - 2 + 9{x^3} - 6{x^2} - 2x - 3\\ = (6 + 9){x^3} + (8 - 6){x^2} + (5 - 2)x + ( - 2 - 3)\\ = 15{x^3} + 2{x^2} + 3x - 5\end{array}\)