Tìm số tự nhiên n để phép chi sau là phép chia hết ;
(14x5-7x3=2x) :7xn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
PT
1
CM
19 tháng 3 2019
x 4 : x n = x 4 - n là phép chia hết nên 4 – n ≥ 0 ⇒ 0 ≤ n ≤ 4
suy ra: n ∈ {0; 1; 2; 3; 4}
PT
1
CM
10 tháng 4 2019
5 x n y 3 : 4 x 2 y 2 = 5/4 x n : x 2 y 3 : y 2 = 5/4 x n - 2 . y là phép chia hết
Suy ra: n – 2 ≥ 0 ⇒ n ≥ 2
CM
29 tháng 6 2017
Vì đa thức 5 x 3 - 7 x 2 + x chia hết cho 3 x n nên mỗi hạng tử của đa thức chia hết cho x n
=> hạng tử x – có số mũ nhỏ nhất của đa thức chia hết cho 3 x n
Do đó, x : x n ⇒ 0 ≤ x ≤ 1 . Vậy n ∈ {0; 1}
CM
26 tháng 11 2017
Vì đa thức 13 x 4 y 3 - 5 x 3 y 3 + 6 x 2 y 2 chia hết cho 5 x n y n nên mỗi hạng tử của đa thức trên chia hết cho 5 x n y n Do đó, hạng tử 6 x 2 y 2 chia hết cho 5 x n y n ⇒ 0 ≤ n ≤ 2 . Vậy n ∈ {0;1;2}
PT
1
CM
1 tháng 12 2017
x n y n + 1 : x 2 y 5 = x n : x 2 y n + 1 : y 5 = x n - 2 . y n - 4 là phép chia hết
H9
HT.Phong (9A5)
CTVHS
6 tháng 10 2023
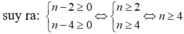
Bài 5.5:
\(\left(2x-3\right)\left(x+1\right)+\left(4x^3-6x^2-6x\right):\left(-2x\right)=18\)
\(\Leftrightarrow\left(2x^2+2x-3x-3\right)+2x\cdot\left(2x^2-3x-3\right):\left(-2x\right)=18\)
\(\Leftrightarrow2x^2-x-3-2x^2+3x+3=18\)
\(\Leftrightarrow2x=18\)
\(\Leftrightarrow x=\dfrac{18}{2}\)
\(\Leftrightarrow x=9\)
Q
1
11 tháng 8 2023
\(\dfrac{3x^{n+1}y^2-2x^5y^n+x^4y^2}{2x^4y^{n-2}}=\dfrac{3}{4}x^{n+1-4}\cdot y^{2-n+2}-x^{5-4}\cdot y^{n-n+2}+\dfrac{1}{2}x^{4-4}\cdot y^{2-n+2}\)
\(=\dfrac{3}{4}x^{n-3}y^{4-n}-xy^2+\dfrac{1}{2}y^{4-n}\)
Để đây là phép chia hết thì n-3>=0 và 4-n>=0
=>3<=n<=4
=>n=3;n=4
đáp án https://goo.gl/BjYiDy
Để phép chia sau là phép chia hết, ta cần thỏa mãn điều kiện là kết quả của phép chia phải là số tự nhiên.
Ta có phép chia: (14x5 - 7x3 = 2x) : 7xn
Để giải phương trình này, ta cần tìm giá trị của n.
Ta thực hiện các bước giải như sau:
Bước 1: Giải phương trình
(14x5 - 7x3 = 2x)
14x5 - 7x3 = 2x
70x - 21x = 2x
49x = 2x
Bước 2: Giải phương trình
49x = 2x
49x - 2x = 0
47x = 0
x = 0
Bước 3: Thay giá trị x = 0 vào phép chia (14x5 - 7x3 = 2x) : 7xn
(14x5 - 7x3 = 2x) : 7xn (14*0 - 7*0 = 2*0) : 7*n*0 0 = 0
Vậy, với mọi giá trị của n, phép chia (14x5 - 7x3 = 2x) : 7xn đều là phép chia hết.
tick cho mik nha