Cho hình bình hành ABCD có AB = 5,2 , BC = 3,5 và góc B = 75 ⁰ . tính diện tích hình bình hành ( vẽ hình )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(8-x>\dfrac{11}{3}\)
=>\(-x>\dfrac{11}{3}-8=-\dfrac{13}{3}\)
=>\(x< \dfrac{13}{3}\)
mà x là số tự nhiên lớn nhất có thể
nên x=4
8 - \(x\) > \(\dfrac{11}{3}\)
suy ra 8 - \(\dfrac{11}{3}\) > \(x\)
\(\dfrac{24}{3}\) - \(\dfrac{11}{3}\) > \(x\)
\(\dfrac{13}{3}\) > \(x\)
4\(\dfrac{1}{3}\) > \(x\)
Vậy \(x\) = 0; 1; 2; 3; 4
Vì \(x\) là số tự nhiên lớn nhất nên \(x\) = 4

\(x^2+2>=2\forall x\)
=>\(\left(x^2+2\right)^2>=4\forall x\)
=>\(-\left(x^2+2\right)^2< =-4\forall x\)
mà \(-\left(y^2-16\right)^4< =0\forall y\)
nên \(-\left(x^2+2\right)^2-\left(y^2-16\right)^4< =-4\forall x,y\)
=>\(B=-\left(x^2+2\right)^2-\left(y^2-16\right)^4+20< =-4+20=16\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x=0\\y^2-16=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y\in\left\{4;-4\right\}\end{matrix}\right.\)

ABCD là hình chữ nhật
=> CD = AB = 4 (cm)
=> AD = BC = 3 (cm)
=> BD = AC = 5 (cm)

Số sách đủ để chia là:
\(3+3=6\left(quyển\right)\)
Tổ được chia 8 quyển nhiều hơn tổ được chia 7 quyển là:
\(8-7=1\left(quyển\right)\)
Số tổ được chia sách là:
\(6:1=6\left(tổ\right)\)
Số sách văn và toán là:
\(7\times6+3=45\left(quyển\right)\) Đ/S:...
Ta có:
\(Q=\dfrac{1}{x^2-4x+11}=\dfrac{1}{\left(x^2-4x+4\right)+7}\\ =\dfrac{1}{\left(x-2\cdot x\cdot2+2^2\right)+7}=\dfrac{1}{\left(x-2\right)^2+7}\)
\(\left(x-2\right)^2\ge0\forall x=>\left(x-2\right)^2+7\ge7\forall x\\ =>Q=\dfrac{1}{\left(x-2\right)^2+7}\le\dfrac{1}{7}\forall x\)
Dấu "=" xảy ra: `x-2=0<=>x=2`

1) 12 ⋮ x => x ∈ Ư(12) = {1; -1; 2; -2; 3; -3; 4; -4; 6; -6; 12; -12}
Mà: x > 2
=> x ∈ {3; 4; 6; 12}
2) 24 ⋮ x => x ∈ Ư(24) = {1; -1; 2; -2; 3; -3; 4; -4; 6; -6; 8; -8; 12; -12; 24; -24}
Mà: x > 4
=> x ∈ {6; 8; 12; 24}
3) 36 ⋮ x => x ∈ Ư(36) = {1; -1; 2; -2; 3; -3; 4; -4; 6; -6; 9; -9; 12; -12; 18; -18; 36; -36}
Mà: x ≥ 3
=> x ∈ {3; 4; 6; 9; 12; 18; 36}
4) 40 ⋮ x => x ∈ Ư(40) = {1; -1; 2; -2; 4; -4; 5; -5; 8; -8; 10; -10; 20; -20; 40; -40}
Mà: x < 10 và x là số tự nhiên
=> x ∈ {1; 2; 4; 8}

\(10x-x^2+2\\
=\left(-x^2+10x-25\right)+27\\
=-\left(x^2-10x+25\right)+27\\
=-\left(x-5\right)^2+27\)
Ta có: \(-\left(x-5\right)^2\le0\forall x=>-\left(x-5\right)^2+27\le27\forall x\)
Dấu "=" xảy ra: `x-5=0<=>x=5`

Bài 1:
A = 8.(32 + 1)(34 + 1)(38 + 1)(316 + 1)
A = (32 - 1)(32 + 1)(34+ 1)(38 +1)(316 + 1)
A = (34 - 1)(34 + 1)(38+ 1)(316 + 1)
A = (38 - 1)(38 + 1)(316 + 1)
A = (316 - 1)(316 +1)
A = (316)2 - 12
A = 332 - 1
1: \(A=8\left(3^2+1\right)\left(3^4+1\right)\cdot...\cdot\left(3^{16}+1\right)\)
\(=\left(3^2-1\right)\left(3^2+1\right)\cdot\left(3^4+1\right)\left(3^8+1\right)\cdot\left(3^{16}+1\right)\)
\(=\left(3^4-1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\)
\(=\left(3^8-1\right)\cdot\left(3^8+1\right)\left(3^{16}+1\right)\)
\(=\left(3^{16}-1\right)\left(3^{16}+1\right)=3^{32}-1\)
2: \(B=\left(1-3\right)\left(3+1\right)\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\)
\(=-\left(3^2-1\right)\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\)
\(=-\left(3^4-1\right)\left(3^4+1\right)\cdot\left(3^8+1\right)\left(3^{16}+1\right)\)
\(=-\left(3^8-1\right)\left(3^8+1\right)\left(3^{16}+1\right)=-\left(3^{16}-1\right)\left(3^{16}+1\right)\)
\(=-\left(3^{32}-1\right)=1-3^{32}\)
3: \(C=24\left(5^2+1\right)\left(5^4+1\right)\cdot...\cdot\left(5^{128}+1\right)+\left(5^{256}-1\right)\)
\(=\left(5^2-1\right)\left(5^2+1\right)\cdot\left(5^4+1\right)\left(5^{128}+1\right)+\left(5^{256}-1\right)\)
\(=\left(5^4-1\right)\cdot\left(5^4+1\right)\cdot...\cdot\left(5^{128}+1\right)+\left(5^{256}-1\right)\)
\(=\left(5^8-1\right)\left(5^8+1\right)\cdot...\cdot\left(5^{128}+1\right)+\left(5^{256}-1\right)\)
\(=\left(5^{16}-1\right)\left(5^{16}+1\right)\cdot...\cdot\left(5^{128}+1\right)+5^{256}-1\)
\(=\left(5^{32}-1\right)\left(5^{32}+1\right)\left(5^{64}+1\right)\left(5^{128}+1\right)+5^{256}-1\)
\(=\left(5^{64}-1\right)\left(5^{64}+1\right)\left(5^{128}+1\right)+5^{256}-1\)
\(=\left(5^{128}-1\right)\left(5^{128}+1\right)+5^{256}-1=2\left(5^{256}-1\right)\)
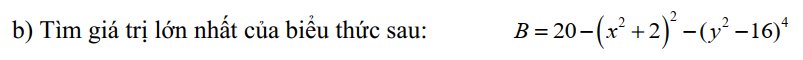
Diện tích tam giác BAC là:
\(S_{BAC}=\dfrac{1}{2}\cdot BA\cdot BC\cdot sinABC=\dfrac{1}{2}\cdot5,2\cdot3,5\cdot sin75=\dfrac{91\sqrt{6}+91\sqrt{2}}{40}\)
ABCD là hình bình hành
=>\(S_{ABCD}=2\cdot S_{BAC}=\dfrac{91\sqrt{6}+91\sqrt{2}}{20}\)