Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

mik cần gấp nha cứu mik
còn bạn nào hcoj giỏi thức ko huhu :((
a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔABH=ΔACK
b: Xét ΔAHK có AH=AK(ΔABH=ΔACK)
nên ΔAHK cân tại A
c: Xét ΔABC có
AK/AB=AH/AC
Do đó: KH//BC

a:ΔABH vuông tại H nên \(\widehat{BAH}+\widehat{ABH}=90^0\)(1)
Ta có: \(\widehat{BAH}+\widehat{KAC}+\widehat{BAC}=180^0\)
=>\(\widehat{BAH}+\widehat{KAC}+90^0=180^0\)
=>\(\widehat{BAH}+\widehat{KAC}=90^0\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{ABH}=\widehat{KAC}\)
Xét ΔHAB vuông tại H và ΔKCA vuông tại K có
AB=CA
\(\widehat{ABH}=\widehat{KAC}\)
Do đó: ΔHAB=ΔKCA
=>AH=CK
b: Ta có: ΔHAB=ΔKCA
=>HB=KA
HK=HA+AK
mà AK=HB và HA=CK
nên HK=HB+CK

a) Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC(ΔABC cân tại A)
\(\widehat{BAH}\) chung
Do đó: ΔAHB=ΔAKC(cạnh huyền-góc nhọn)
Suy ra: AH=AK(hai cạnh tương ứng)

a) Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC(ΔABC cân tại A)
\(\widehat{BAH}\) chung
Do đó: ΔAHB=ΔAKC(cạnh huyền-góc nhọn)
Suy ra: AH=AK(hai cạnh tương ứng)

a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc HAB chung
=>ΔAHB=ΔAKC
=>AH=AK
b:
Xét ΔABC có
BH,CK là đường cao
BH cắt CK tại I
=>I là trực tâm
=>AI vuông góc BC tại M
Xét ΔKBC vuông tạiK và ΔHCB vuông tại H có
BC chung
KC=HB
=>ΔKBC=ΔHCB
=>góc IBC=góc ICB
=>ΔIBC cân tại I
mà IM là đường cao
nên IM là phân giác
c: Xet ΔBAC có AK/AB=AH/AC
nên KH//BC

a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
Do đó: ΔAHB=ΔAKC
b: ΔAHB=ΔAKC
=>AH=AK
c: Xét ΔAKI vuông tại K và ΔAHI vuông tại H co
AI chung
AH=AK
Do đó: ΔAKI=ΔAHI
=>góc KAI=góc HAI
=>AI là phân giác của góc BAC

`a)`
Có `Delta ABC` cân tại `A=>AB=AC`
Xét `Delta ABH` và `Delta ACK` có :
`hat(AHB)=hat(AKC)(=90^0)`
`hat(A)-chung`
`AB=AC(cmt)`
`=>Delta ABH=Delota ACK(c.h-g.n)`
`b)`
Xét `Delta BHC` và `Delta CKB` có :
`hat(BHC)=hat(CKB)(=90^0)`
`hat(KBC)=hat(HCB)(hat(ABC)=hat(ACB))`
`BC-chung`
`=>Delta BHC=Delta CKB(c.h-g.n)`
`c)`
Có `Delta ABH= Delta ACK(cmt)=>AH=AK` ( 2 cạnh t/ứng )
`=>Delta AHK` cân tại `A=>hat(AHK)=(180^0-hat(A))/2`
`Delta ABC ` cân tại `A=>hat(ACB)=(180^0-hat(A))/2`
mà `2` góc này ở vị trí đ/vị
nên `KH//BC`
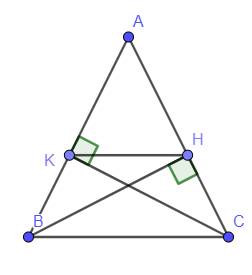
a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K co
AB=AC
góc A chung
=>ΔAHB=ΔAKC
b: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
KC=HB
=>ΔKCB=ΔHBC
c: Xét ΔABC có AK/AB=AH/AC
nên KH//CB