Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
Gọi I là điểm sao cho
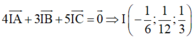
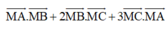
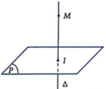
khi và chỉ khi M là hình chiếu của I lên mặt phẳng (Oxy)
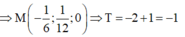
Đáp án D
Gọi I(a; b; c) thỏa mãn
Khi đó
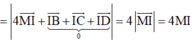
Suy ra MI min => M là hình chiếu của I trên (Oyz) => M(0;1;4)
Chọn D
Vậy M là hình chiếu vuông góc của G lên mặt phẳng (Oyz) nên M (0;1;4)
Đáp án C
Gọi G là trọng tâm của tam giác ABC => G(2;1;3)
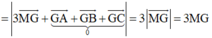
Suy ra MG min <=>M là hình chiếu của G trên (Oxy) => M(2;1;0)
Đáp án C
Gọi I là trung điểm của BC ⇒ I 5 2 ; - 1 2 ; 1 và E thỏa mãn
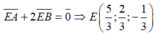
Khi đó
Dễ thấy I, E nằm cùng phía với mặt phẳng (Oyz)
Gọi F là điểm đối xứng E qua mp (Oyz) ⇒ F - 5 3 ; 2 3 ; - 1 3
Do đó
Chọn D
Gọi M (x;y;z).
Ta có MA = 2MB nên (x-1)²+ (y-2)²+ (z-3)² = 4 [ x²+ (y-4)²+ (z-5)² ]
Suy ra tập hợp các điểm M thỏa mãn MA = 2MB là mặt cầu (S) có tâm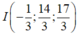 
và bán kính 
Vì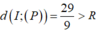 
nên (P) không cắt (S).
Do đó, khoảng cách từ điểm M đến mặt phẳng (P): 2x-2y-z+6 = 0 đạt giá trị nhỏ nhất là:
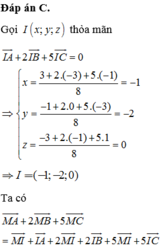
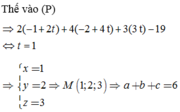
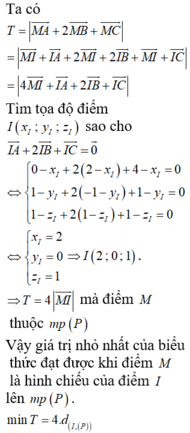
Gọi \(I\left(a;b;c\right)\) là điểm sao cho \(\overrightarrow{IA}-2\overrightarrow{IB}-\overrightarrow{IC}=\overrightarrow{0}\)
\(\lrArr\left(2-a;1-b;-3-c\right)-2\left(1-a;-2-b;-1-c\right)-\left(-2-a;1-b;2-c\right)=\left(0;0;0\right)\)
\(\lrArr\begin{cases}2-a-2+2a+2+a=0\\ 1-b+4+2b-1+b=0\\ -3-c+2+2c-2+c=0\end{cases}\)
\(\lrArr\begin{cases}a=-1\\ b=-2\\ c=\frac32\end{cases}\)
\(\rArr I\left(-1;-2;\frac32\right)\)
Khi đó \(P=\left|\overrightarrow{MA}-2\overrightarrow{MB}-\overrightarrow{MC}\right|\)
\(=\left|\left(\overrightarrow{MI}+\overrightarrow{IA}\right)-2\left(\overrightarrow{MI}+\overrightarrow{IB}\right)-\left(\overrightarrow{MI}+\overrightarrow{IC}\right)\right|\)
\(=\left|-2\overrightarrow{MI}+\overrightarrow{IA}-2\overrightarrow{IB}-\overrightarrow{IC}\right|\)
\(=2MI\)
Để P đạt GTNN thì MI đạt GTNN \(\rArr\) M là hình chiếu của I lên trục Ox \(\rArr M\left(-1;0;0\right)\)
Vậy M(-1; 0; 0)