
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(y^2=5-\left|x-1\right|\)
=> \(y^2\le5\)
Mà y^2 là số chính phương.
=> \(y^2=0\)hoặc \(y^2=1\)hoặc \(y^2\)=4
+) Với \(y^2=0\)=> y = 0
và \(5-\left|x-1\right|=0\)
<=> \(\left|x-1\right|=5\)
<=> x - 1 = 5 hoặc x - 1 = - 5
<=> x = 6 hoặc x = -4
+) Với \(y^2=1\)=> y = \(\pm1\)
và \(5-\left|x-1\right|=1\)
<=> \(\left|x-1\right|=4\)
<=> x - 1 = 4 hoặc x - 1 = - 4
<=> x = 5 hoặc x = -3
+) Với \(y^2=4\)=> y = \(\pm2\)
và \(5-\left|x-1\right|=4\)
<=> \(\left|x-1\right|=1\)
<=> x - 1 = 1 hoặc x - 1 = - 1
<=> x = 2 hoặc x = 0
Kết luận:...
Trường hợp x, y là số thực:
\(5-\left|x-1\right|=y^2\ge0\)
=> \(\left|x-1\right|\le5\)
=> \(-5\le x-1\le5\)
=> \(-4\le x\le6\)
Với \(-4\le x\le6\) khi đó: \(y=\sqrt{5-\left|x-1\right|}\)
Vậy tập nghiệm x, y là: \(S=\left\{\left(x;y\right):-4\le x\le6;y=\sqrt{5-\left|x-1\right|}\right\}\)

Bài 1:
a: =237+(1999-1499)-(174+226)
=237+1500-1400
=237+1100
=1337
b: =-137,5(1+52+47)
=-137,5x100
=-13750
Bài 3:
a: Số học sinh nữ bằng:
6/(5+6)=6/11(phần)
b: Số học sinh nữ là:
1210x6/11=660(bạn)
Số học sinh nam là:
1210-660=550(bạn)

Phương pháp:
+) Lấy loganepe hai vế, đưa phương trình về dạng phương trình bậc hai ẩn x.
+) Tìm điều kiện để phương trình có 2 nghiệm. Áp dụng định lí Vi-ét.
+) Sử dụng BĐT Cô-si cho 3 số không âm đánh giá biểu thức S.
Cách giải:

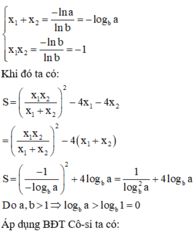
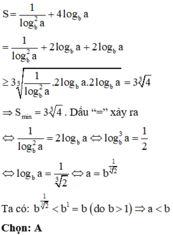

Đáp án C
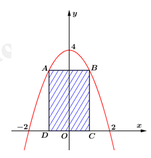 Gọi S là diện tích hình phẳng giới hạn bởi Parabol có phương trình
y
=
4
-
x
2
và trục hoành
Gọi S là diện tích hình phẳng giới hạn bởi Parabol có phương trình
y
=
4
-
x
2
và trục hoành
Suy ra ∫ - 2 2 4 - x 2 d x = 32 3 m 2
Gọi điểm C a ; 0 , a > 0 ⇒ D - a ; 0 B ( a ; 4 - a 2 ) , A - a ; 4 - a 2
Gọi S 1 là diện tích ABCD, suy ra S 1 = A B . B C = 2 a . 4 - a 2 m 2
Gọi S 2 là diện tích có hoa văn, suy ra S 2 = S - S 1
S 2 nhỏ nhất khi và chỉ khi S 1 lớn nhất
Xét hàm số f a = 2 a 4 - a 2 , a ∈ 0 ; 4
Ta có f ' a = 8 - 6 a 2 ⇒ f ' a = 0 ⇔ a = 2 3
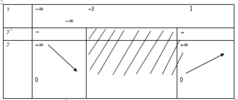
Xét bảng biến thiên hàm số f(a) với a ∈ 0 ; 4
Suy ra m a x 0 ; 4 f a = f 2 3 = 32 3 9 m 2 . Suy ra S 2 m i n = 32 3 - 32 3 9 ≈ 4 , 51 m 2
Suy ra số tiền cần bằng 902.000 đồng.

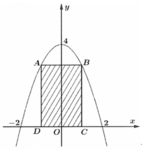
Chọn hệ trục tọa độ như hình vẽ. Khi đó phương trình Parabol có dạng:
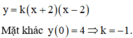
Gọi là diện tích hình phẳng giới hạn bởi Parabol có phương trình y = 4 - x 2 và trục hoành.

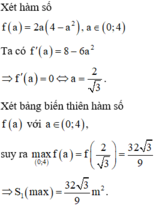

Ta gọi số bị trừ và số trừ la a và b(a>b). Ta có:
a-b=1217 và 4b-a=376
Vậy a-b+4b-a=1217+376
3b = 1593
b = 1593 :3
b = 531
=>a= 1217+531=1748
Vậy số bị trừ là 1748
số trừ là 531

Ta có hệ giao điểm như sau
1 + m t ' = t + 5 3 + t ' = 2 t + 3 - 5 + m t ' = - t + 3 ⇒ t ' = 2 t 2 m t + 1 = t + 5 2 m t - 5 = - t + 3 ⇔ 2 m - 1 t = 4 2 m + 1 t = 8
Hệ có nghiệm duy nhất ⇔ 4 2 m - 1 = 8 2 m + 1 ⇔ m = 3 2
Vậy m là một số hữu tỉ dương.
Đáp án C
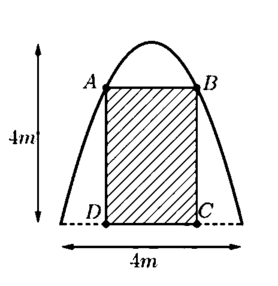 Chi phí dán hoa văn là 200.000 đồng cho một
m
2
bảng. Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên pano sẽ là bao nhiêu (làm tròn đến hàng nghìn)?
Chi phí dán hoa văn là 200.000 đồng cho một
m
2
bảng. Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên pano sẽ là bao nhiêu (làm tròn đến hàng nghìn)?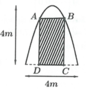

khi chúng ta ko bt làm
Phép toán 4:3 = 2 có thể đúng trong trường hợp biểu diễn ở hệ đếm cơ số 5. Trong hệ cơ số 5, số 4 chia cho số 3 sẽ cho kết quả là 2.
đúng thì tick cho mình với.