K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Z
QA
5 tháng 2 2022
Trả lời:
a, \(x^2-6x+11=x^2-6x+9+2=\left(x-3\right)^2+2\ge2\forall x\)
Dấu "=" xảy ra khi x - 3 = 0 <=> x = 3
Vậy GTNN của biểu thức bằng 2 khi x = 3
b, \(-x^2+6x-11=-\left(x^2-6x+11\right)=-\left(x^2-6x+9+2\right)=-\left[\left(x-3\right)^2+2\right]\)
\(=-\left(x-3\right)^2-2\le-2\forall x\)
Dấu "=" xảy ra khi x - 3 = 0 <=> x = 3
Vậy GTLN của biểu thức bằng - 2 khi x = 3
c, \(x^2+2x+2=x^2+2x+1+1=\left(x+1\right)^2+1\ge1>0\forall x\inℤ\) (đpcm)
Dấu "=" xảy ra khi x + 1 = 0 <=> x = - 1
8 tháng 10 2023
a: \(x^2+x+1=x^2+x+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}>0\forall x\)
b: \(4y^2+2y+1\)
\(=4\left(y^2+\dfrac{1}{2}y+\dfrac{1}{4}\right)\)
\(=4\left(y^2+2\cdot y\cdot\dfrac{1}{4}+\dfrac{1}{16}+\dfrac{3}{16}\right)\)
\(=4\left(y+\dfrac{1}{4}\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}>0\forall y\)
c: \(-2x^2+6x-10\)
\(=-2\left(x^2-3x+5\right)\)
\(=-2\left(x^2-3x+\dfrac{9}{4}+\dfrac{11}{4}\right)\)
\(=-2\left(x-\dfrac{3}{2}\right)^2-\dfrac{11}{2}< =-\dfrac{11}{2}< 0\forall x\)
8 tháng 10 2023
`#3107.101107`
a)
`x^2 + x + 1`
`= (x^2 + 2*x*1/2 + 1/4) + 3/4`
`= (x + 1/2)^2 + 3/4`
Vì `(x + 1/2)^2 \ge 0` `AA` `x`
`=> (x + 1/2)^2 + 3/4 \ge 3/4` `AA` `x`
Vậy, `x^2 + x + 1 > 0` `AA` `x`
b)
`4y^2 + 2y + 1`
`= [(2y)^2 + 2*2y*1/2 + 1/4] + 3/4`
`= (2y + 1/2)^2 + 3/4`
Vì `(2y + 1/2)^2 \ge 0` `AA` `y`
`=> (2y + 1/2)^2 + 3/4 \ge 3/4` `AA` `y`
Vậy, `4y^2 + 2y + 1 > 0` `AA` `y`
c)
`-2x^2 + 6x - 10`
`= -(2x^2 - 6x + 10)`
`= -2(x^2 - 3x + 5)`
`= -2[ (x^2 - 2*x*3/2 + 9/4) + 11/4]`
`= -2[ (x - 3/2)^2 + 11/4]`
`= -2(x - 3/2)^2 - 11/2`
Vì `-2(x - 3/2)^2 \le 0` `AA` `x`
`=> -2(x - 3/2)^2 - 11/2 \le 11/2` `AA` `x`
Vậy, `-2x^2 + 6x - 10 < 0` `AA `x.`
CM
18 tháng 8 2018
Ta có: x 2 – 6x + 10 = x 2 – 2.x.3 + 9 + 1 = x - 3 2 + 1
Vì x - 3 2 ≥ 0 với mọi x nên x - 3 2 + 1 > 0 mọi x
Vậy x 2 – 6x + 10 > 0 với mọi x.(đpcm)
NC
23 tháng 8 2020
1) \(A=x^2+2x+2=\left(x+1\right)^2+1\ge1>0\left(\forall x\right)\)
2) \(B=x^2+6x+11=\left(x+3\right)^2+2\ge2>0\left(\forall x\right)\)
3) \(C=4x^2+4x-2=\left(2x+1\right)^2-2\ge-2\) chưa chắc nhỏ hơn 0
4) \(D=-x^2-6x-11=-\left(x+3\right)^2-2\le-2< 0\left(\forall x\right)\)
5) \(E=-4x^2+4x-2=-\left(2x-1\right)^2-1\le-1< 0\left(\forall x\right)\)
KN
23 tháng 8 2020
1. \(A=x^2+2x+2=\left(x+1\right)^2+1\)
Vì \(\left(x+1\right)^2\ge0\forall x\)\(\Rightarrow\left(x+1\right)^2+1\ge1\)
=> Đpcm
2. \(B=x^2+6x+11=\left(x+3\right)^2+2\)
Vì \(\left(x+3\right)^2\ge0\forall x\)\(\Rightarrow\left(x+3\right)^2+2\ge2\)
=> Đpcm
3. \(C=4x^2+4x-2=-\left(4x^2-4x+2\right)\)
\(=-\left(4\left(x-\frac{1}{2}\right)^2+1\right)\)
Vì \(\left(x-\frac{1}{2}\right)^2\ge0\forall x\Rightarrow4\left(x-\frac{1}{2}\right)^2+1\ge1\)
\(\Rightarrow-\left(4\left(x-\frac{1}{2}\right)^2+1\right)\le1\)
=> Đpcm
4,5 làm tương tự
T
24 tháng 9 2023
\(x^2-5x+7\)
\(=x^2-2\cdot x\cdot\dfrac{5}{2}+\left(\dfrac{5}{2}\right)^2-\dfrac{25}{4}+7\)
\(=\left(x-\dfrac{5}{2}\right)^2+\dfrac{3}{4}\)
Ta thấy: \(\left(x-\dfrac{5}{2}\right)^2\ge0\forall x\)
\(\Rightarrow\left(x-\dfrac{5}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}>0\forall x\)
hay \(x^2-5x+7>0\forall x\).
Vậy ...
#\(Toru\)
6 tháng 12 2021
b: \(=\left(x-5\right)^2-9y^2\)
\(=\left(x-5-3y\right)\left(x-5+3y\right)\)
6 tháng 12 2021
Bài 1:
b: \(=\left(x-5\right)^2-9y^2\)
\(=\left(x-5-3y\right)\left(x-5+3y\right)\)
7 tháng 12 2021
\(1,\\ a,=3x\left(x-3y\right)\\ b,=\left(x-5\right)^2-9y^2=\left(x-3y-5\right)\left(x+3y-5\right)\\ c,=3x\left(x-y\right)-2\left(x-y\right)=\left(3x-2\right)\left(x-y\right)\\ 2,\\ Sửa:x^2-6x+10=\left(x-3\right)^2+1\ge1>0,\forall x\)
CD
7 tháng 12 2021
1, =3x (2x -3y)
c, = 3x(x-y) -2(x-y)
= (3x-2)(x-y)
2, Ta có: x2 -6x+10= (x-3)2 +11
Nhận xét: (x-3)2 >= 0 với mọi số thực x
=> (x-3)2 +1 >= 1 >0 (đpcm)
PT
1
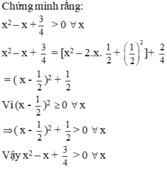
Đặt: \(B=-x^2+6x-11\)
\(B=-\left(x^2-6x+11\right)\)
\(B=-\left(x^2-2.x.3+9+2\right)\)
\(B=-\left[\left(x-3\right)^2+2\right]\)
\(B=-\left(x-3\right)^2-2\)
Ta có: \(-\left(x-3\right)^2\le0\) với mọi x
\(-\left(x-3\right)^2-2< 0\) với mọi x
Hay \(B< 0\) với mọi x. (đpcm)
\(#NqHahh\)
hom nay moi di khai giang ve ma da co bai roi ha