Question

[Nguyễn Quang Thắng]

 

Nghiệm của phương trình cosx + sinx = 1 là

Answer 1

[Lê Song Phương]

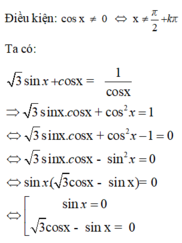
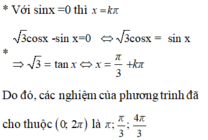
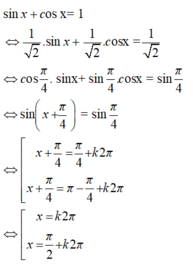
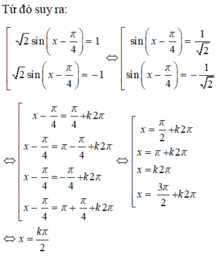
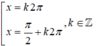
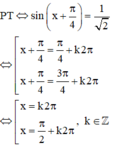
\(cosx+sinx=1\)

\(\Leftrightarrow\dfrac{\sqrt{2}}{2}cosx+\dfrac{\sqrt{2}}{2}sinx=\dfrac{\sqrt{2}}{2}\)

\(\Leftrightarrow sin\left(\dfrac{\pi}{4}\right)cosx+cos\left(\dfrac{\pi}{4}\right)sinx=\dfrac{\sqrt{2}}{2}\)

\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=sin\left(\dfrac{\pi}{4}\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=\dfrac{\pi}{4}+2k\pi\\x+\dfrac{\pi}{4}=\pi-\dfrac{\pi}{4}+2k\pi\end{matrix}\right.\left(k\inℤ\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2k\pi\\x=\dfrac{\pi}{2}+2k\pi\end{matrix}\right.\left(k\inℤ\right)\)

Vậy tập nghiệm của pt đã cho là \(S=\left\{2k\pi|k\inℤ\right\}\cup\left\{\dfrac{\pi}{2}+2k\pi|k\inℤ\right\}\)