Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi B là một điểm nằm trên thanh ngang và H là hình chiếu vuông góc xuống mặt dốc.
Vì dốc nghiêng 150 so với phương nằm ngang nên nên góc giữa cột và mặt phẳng dốc bằng 750
Khoảng cách từ B đến mặt phẳng dốc là:
\(BH=2.28\cdot sin75\simeq2,2\left(m\right)\)
=>Không cho phép xe cao 2,21m đi qua cầu

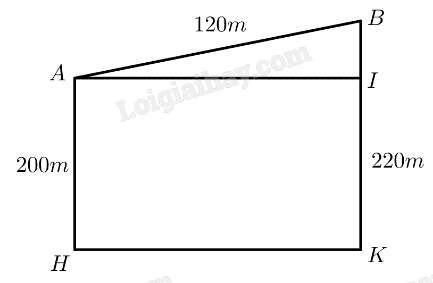
Mô hình hoá như hình vẽ, với \(AB\) là chiều dài con dốc, \(AH\) là độ cao của điểm \(A\) so với mặt nước biển, \(BK\) là độ cao của điểm \(B\) so với mặt nước biển, \(BI\) là chiều cao của con dốc, độ lớn của góc \(\widehat {BAI}\) chỉ độ dốc.
Ta có: \(AH = 200,BK = 220,AB = 120\).
\(AHKB\) là hình chữ nhật \( \Rightarrow IK = AH = 200 \Rightarrow BI = BK - IK = 220 - 200 = 20\)
Vì tam giác \(ABI\) vuông tại \(I\) nên ta có:
\(\sin \widehat {ABI} = \frac{{BI}}{{AB}} = \frac{{20}}{{120}} = \frac{1}{6} \Rightarrow \widehat {ABI} \approx 9,{59^ \circ }\) tương ứng với 10,66%
Vậy độ dốc của con dốc đó là 10,66%.

a, Vì gốc tọa độ đặt tại P nên P(0;0) do đó ta có \(c=y\left(0\right)=0\)
b, \(y'=2ax+b\Rightarrow y'\left(0\right)=b\)
Mà L1 là phương trình tiếp tuyến tại P có hệ số góc là 0,5 nên \(y'\left(0\right)=0,5\Rightarrow b=0,5\)
c, L2 là phương trình tiếp tuyến tại Q có hệ số góc -0,75 nên \(y'\left(x_Q\right)=2ax_Q+0,5=-0,75\)
Vì khoảng cách theo phương ngang giữa P và Q là 40m nên \(x_Q-x_P=x_Q=40\)
\(\Rightarrow2a\cdot40+0,5=-0,75\\ \Leftrightarrow a=-\dfrac{1}{64}\)
d, \(y_Q=-\dfrac{1}{64}\cdot40^2+0,5\cdot40=-5\)
Vậy chênh lệch độ cao giữa hai điểm chuyển tiếp P và Q là \(\left|y_P-y_Q\right|=5\)

Chọn đáp án B
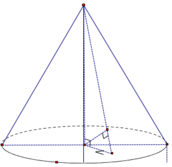
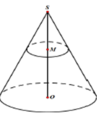
Gọi I là trung điểm AB.
Ta có
![]()
Trong (SOI), kẻ OH ⊥ SI thì OH ⊥ (SAB)
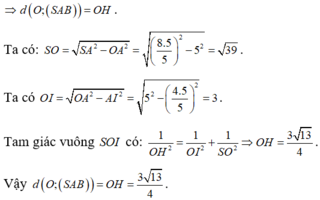

Đáp án B.
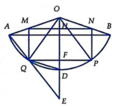
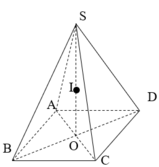
Qua O kẻ đường thẳng vuông góc với MN, đường thẳng này cắt MN, PQ, cung AB,AQ lần lượt tại
Độ dài cung AB là chu vi đường tròn đáy của hình nón nên
![]()
Lại có
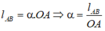
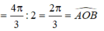
Áp dụng định lý cosin trong tam giác OAB có
![]()
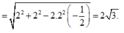
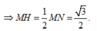
Do OD
⊥
AB nên OD là tia phân giác của ![]() . Xét tam giác vuông OMH có OH =
. Xét tam giác vuông OMH có OH =
![]()
Xét tam giác OPQ có
![]()
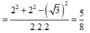
Mà
![]()
![]()
![]()
Xét tam giác DOQ có:
![]()
![]()
Xét tam giác vuông DQF có
![]()
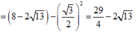
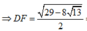
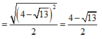
=> HF = OD - OH - DF =
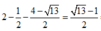
= MQ - NP
Gọi R là bán kính đáy của hình trụ tạo bởi hình chữ nhật MNPQ. Chu vi đáy của hình trụ chính là độ dài của PQ nên
![]()
Khi đó thể tích khối trụ tạo ra bởi hình chữ nhật MNPQ là:
![]()
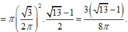


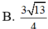
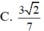
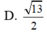
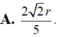
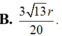
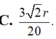
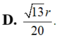

Cắt hình nón theo đường sinh OA và trải ra mặt phẳng ta đương hình quạt như hình vẽ sau
Ta có góc ở đỉnh của hình quạt là \(\dfrac{2\pi\cdot200}{600}=\dfrac{2\pi}{3}\)
Lại có, con đường từ A đến B ngắn nhất => AB là đoạn thẳng
Từ đó, đỉnh dốc H cao nhất nên gần đỉnh O => H là hình chiếu vuông góc của O lên AB
Áp dụng định lý cosin trong tam giác OAB ta có:
\(AB=\sqrt{OA^2+OB^2-2OA.OB.cos\left(\dfrac{2\pi}{3}\right)}=10\sqrt{91}\)
\(cosOBA=\dfrac{OB^2+BA^2-OA^2}{2\cdot OB\cdot OA}\)
\(HB=OB.cosOBH=OB.\left(\dfrac{OB^2+BA^2-ÓA^2}{2\cdot OA\cdot OB}\right)=\dfrac{400}{\sqrt{91}}\)Vậy quãng đường xuống dốc là \(HB=\dfrac{400}{\sqrt{91}}\)