Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

d)\(\frac{2.3+4.6+14.21}{3.5+6.10+21.35}=\frac{2.3+2.2.6+2.7.21}{3.5+3.2.10+3.7.35}=\frac{2.3+2.12+2.147}{3.5+3.20+3.245}=\frac{2\left(3+12+147\right)}{3\left(5+20+245\right)}\)
\(=\frac{2.162}{3.270}=\frac{54}{135}=\frac{2}{5}\)
\(a.\frac{-2019.2018+1}{\left(-2017\right).\left(-2019\right)+2018}\)
\(=\frac{2019.\left(-2018\right)+1}{2019.2017+2018}\)
\(=\frac{2019.\left(-2018\right)+1}{2019.2018-1}\)
\(=-\frac{2018}{2018}\)
\(=-1\)

Ta có : \(\dfrac{2017+2018}{2018+2019}=\dfrac{2017}{2018+2019}+\dfrac{2018}{2018+2019}\)
Rõ ràng ta thấy : \(\dfrac{2017}{2018}>\dfrac{2017}{2018+2019}\) (1)
\(\dfrac{2018}{2019}>\dfrac{2018}{2018+2019}\) (2)
Từ (1) và (2), suy ra :
\(\dfrac{2017}{2018}+\dfrac{2018}{2019}>\dfrac{2017+2018}{2018+2019}\)
Vậy ......................
~ Học tốt ~
Ta có : \(\dfrac{2017}{2018}+\dfrac{2018}{2019}+\dfrac{2019}{2020}=\left(1-\dfrac{1}{2018}\right)+\left(1-\dfrac{1}{2019}\right)+\left(1-\dfrac{1}{2020}\right)\)\(=\left(1+1+1\right)-\left(\dfrac{1}{2018}+\dfrac{1}{2019}+\dfrac{1}{2020}\right)\)
\(=3+\left(\dfrac{1}{2018}+\dfrac{1}{2019}+\dfrac{1}{2020}\right)< 3\)
Vậy \(\dfrac{2017}{2018}+\dfrac{2018}{2019}+\dfrac{2019}{2020}< 3\)

a)\(\dfrac{-3}{29}+\dfrac{16}{58}\)\(=\dfrac{-3}{29}+\dfrac{8}{29}=\dfrac{5}{29}\)
b) \(\dfrac{8}{40}+\dfrac{-36}{45}=\dfrac{1}{5}+\dfrac{-4}{5}=\dfrac{-3}{5}\)
c) \(\dfrac{-8}{18}+\dfrac{-15}{27}=\dfrac{-4}{9}+\dfrac{-5}{9}=\dfrac{-9}{9}=-1\)
a) \(\dfrac{-3}{29}+\dfrac{16}{58}=\dfrac{-3}{29}+\dfrac{8}{29}=\dfrac{-3+8}{29}=\dfrac{5}{29}\)
b) \(\dfrac{8}{40}+\dfrac{-36}{45}=\dfrac{1}{5}+\dfrac{-4}{5}=\dfrac{1+\left(-4\right)}{5}=\dfrac{-3}{5}\)
c) \(\dfrac{-8}{18}+\dfrac{-15}{27}=\dfrac{-4}{9}+\dfrac{-5}{9}=\dfrac{-4+\left(-5\right)}{9}=\dfrac{-9}{9}=-1\)

Giải:
Ta có:
\(\dfrac{a}{b}=\dfrac{-8}{11}\left(1\right)\Leftrightarrow1-\dfrac{a}{b}=1-\dfrac{-8}{11}\)
Hay \(\dfrac{b-a}{b}=\dfrac{11+8}{11}=\dfrac{19}{11}\left(2\right)\)
Thay \(b-a=190\) vào \(\left(2\right)\) ta được:
\(\dfrac{190}{b}=\dfrac{19}{11}\Leftrightarrow190.11=19b\Leftrightarrow b=110\)
Thay \(b=110\) vào \(\left(1\right)\) ta được:
\(\dfrac{a}{110}=\dfrac{-8}{11}\Leftrightarrow11a=-8.110\Leftrightarrow a=-80\)
Vậy phân số \(\dfrac{a}{b}\) cần tìm là \(\dfrac{-80}{110}\)
Thay b - a = 190 vào (1) ta được:
Phân số a/b phải tìm là -80/110

3. Gọi d là ƯCLN(2n + 3, 4n + 8), d ∈ N*
\(\Rightarrow\hept{\begin{cases}2n+3⋮d\\4n+8⋮d\end{cases}\Rightarrow\hept{\begin{cases}2\left(2n+3\right)⋮d\\4n+8⋮d\end{cases}\Rightarrow}\hept{\begin{cases}4n+6⋮d\\4n+8⋮d\end{cases}}}\)
\(\Rightarrow\left(4n+8\right)-\left(4n+6\right)⋮d\)
\(\Rightarrow2⋮d\)
\(\Rightarrow d\in\left\{1;2\right\}\)
Mà 2n + 3 không chia hết cho 2
\(\Rightarrow d=1\)
\(\RightarrowƯCLN\left(2n+3,4n+8\right)=1\)
\(\Rightarrow\frac{2n+3}{4n+8}\) là phân số tối giản.

a) \(\frac{25}{1188}\)
b)\(\frac{4}{3}\)
c)\(\frac{17\times4}{-17}=\frac{4}{-1}=\frac{-4}{1}=-4\)

Tính các tổng dưới đây sau khi đã rút gọn phân số :
a)\(\dfrac{7}{21}\) + \(\dfrac{9}{-36}\) = \(\dfrac{7}{21}\)+\(\dfrac{-9}{36}\)=\(\dfrac{1}{3}\)+\(\dfrac{-1}{4}\)=\(\dfrac{4}{12}\)+\(\dfrac{-3}{12}\)=\(\dfrac{1}{12}\)
b) \(\dfrac{-12}{18}\)+\(\dfrac{-21}{35}\)=\(\dfrac{-2}{3}\)+\(\dfrac{-3}{5}\)=\(\dfrac{-10}{15}\)+\(\dfrac{-9}{15}\)=\(\dfrac{-19}{15}\)
c) \(\dfrac{-3}{21}\)+\(\dfrac{6}{42}\)=\(\dfrac{-1}{7}\)+\(\dfrac{1}{7}\)=0
d) \(\dfrac{-18}{24}\)+\(\dfrac{15}{-21}\)=\(\dfrac{-18}{24}\)+\(\dfrac{-15}{21}\)=\(\dfrac{-3}{4}\)+\(\dfrac{-5}{7}\)=\(\dfrac{-21}{28}\)+\(\dfrac{-20}{28}\)=\(\dfrac{-41}{28}\)

Vì cộng cả tử và mẫu của phân số \(\dfrac{23}{40}\) với cùng một số tự nhiên n rồi rút gọn ta được \(\dfrac{3}{4}\) nên ta được:
\(\dfrac{23+n}{40+n}=\dfrac{3}{4}\)
\(\Rightarrow\)\(4.\left(23+n\right)=3.\left(40+n\right)\)
hay 92 + 4.n = 120 + 3.n
4.n - 3.n = 120 - 92
\(\Rightarrow\) n = 28
Vậy số tự nhiên n cần tìm là 28
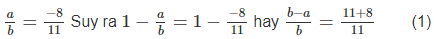
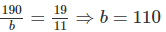
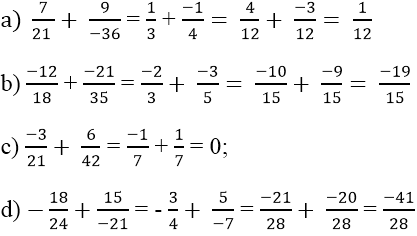
\(\dfrac{3^{2019}}{3^{2017}}=\dfrac{3^{2017}\cdot3\cdot3}{3^{2017}}=\dfrac{3\cdot3}{1}=9\)
viết ra thành 3.3.3.3.....
=9