
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét ΔPOQ có OP=OQ=PQ
nên ΔOPQ đều
=>góc POQ=60 độ
=>góc NOQ=30 độ

a) Xét ΔOAB có OA=OB=AB(=R)
nên ΔOAB đều(Dấu hiệu nhận biết tam giác đều)
\(\Leftrightarrow\widehat{AOB}=60^0\)
\(\Leftrightarrow sđ\stackrel\frown{AB}=60^0\)

a) Xét ΔOAB có OA=OB=AB(=R)
nên ΔOAB đều(Dấu hiệu nhận biết tam giác đều)
\(\Leftrightarrow\widehat{AOB}=60^0\)
hay \(sđ\stackrel\frown{AB}=60^0\)

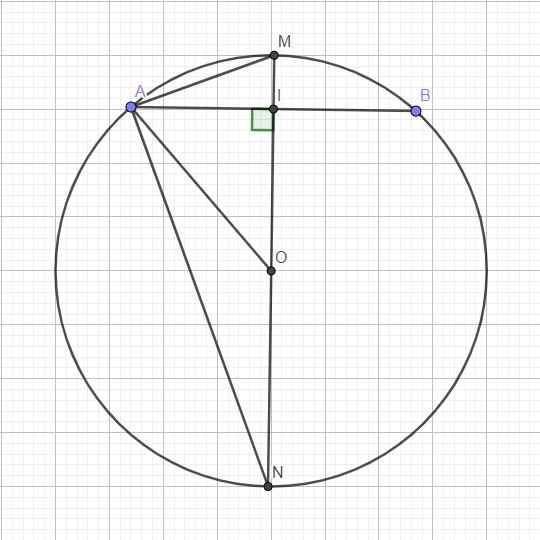
Do I là trung điểm AB \(\Rightarrow OI\perp AB\)
\(AI=\dfrac{1}{2}AB=3\)
Trong tam giác vuông OAI, áp dụng Pitago:
\(OI=\sqrt{OA^2-AI^2}=\sqrt{R^2-AI^2}=4\)
\(\Rightarrow IM=OM-OI=R-OI=1\)
\(\Rightarrow AM=\sqrt{AI^2+IM^2}=\sqrt{10}\left(cm\right)\)
b.
Vẫn như trên, ta có: \(AI=\dfrac{1}{2}AB=6\)
Do MN là đường kính \(\Rightarrow\Delta MAN\) vuông tại A
Áp dụng hệ thức lượng trong tam giác vuông MAN với đường cao AI:
\(\dfrac{1}{AI^2}=\dfrac{1}{AN^2}+\dfrac{1}{AM^2}\Rightarrow\dfrac{1}{6^2}=\dfrac{1}{10^2}+\dfrac{1}{AM^2}\Rightarrow AM=\dfrac{15}{2}\)
Áp dụng hệ thức lượng:
\(AI.MN=AN.AM\Leftrightarrow MN=\dfrac{AM.AN}{AI}=\dfrac{25}{2}\)
\(\Rightarrow R=\dfrac{MN}{2}=\dfrac{25}{4}\left(cm\right)\)

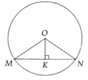
a, Tính được OK = R 2
b, Tính được
M
O
K
^
=
60
0
;
M
O
N
^
=
120
0
c, HS tự làm

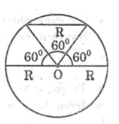
Vì hai cung không phải là cung lớn nên nó có thể là cung nhỏ hoặc cung nửa đường tròn
Cung nửa đường tròn có số đo bằng 180 ° và dây căng cung bằng 2R
Cung 60 ° có dây căng cung là R
Vậy cung nửa đường tròn và cung 60 ° thỏa mãn bài toán




ĐK:x≥1. Chứng minh y≥0
trải lời đi nhanh lên